Määrätyn integraalin sovelluksia

Määrätyn integraalin avulla voidaan laskea funktioiden kuvaajien rajoittamia pinta-aloja. Käytännössä lasku voisi tuottaa esimerkiksi tiettynä aikavälinä kuljetun matkan, kun etenemisnopeus vaihtelee. Tarkastellaan tässä muutamia hieman erilaisia määrätyn integraalin sovelluksia.

Käyrien välisiä pinta-aloja

Tähän asti määrätyn integraalin avulla on laskettu pinta-aloja funktion \(f(x)\) kuvaajan ja vaaka-akselin välillä, kun alue rajataan kahdella suoralla \(x=x_1\) ja \(x=x_2\). Pinta-aloja voidaan laskea myös kahden funktion, \(f(x)\) ja \(g(x)\), väliltä.

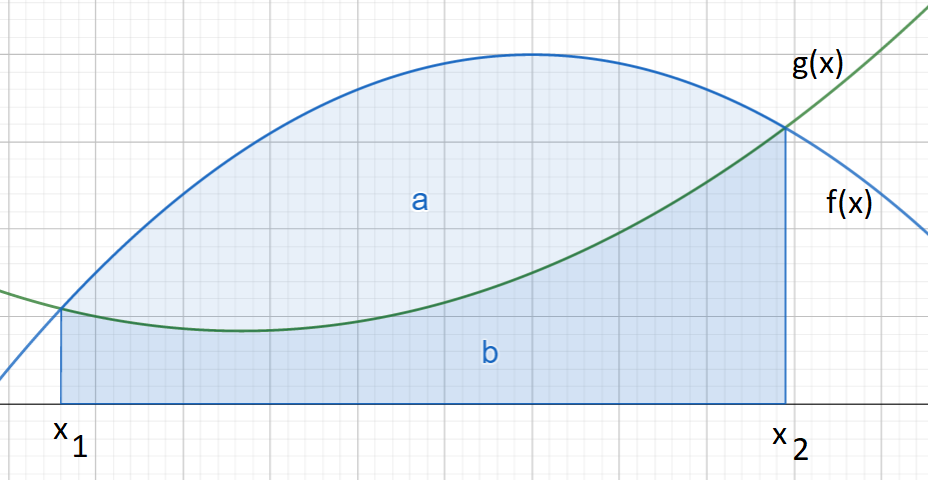
Tarkastellaan kuvan mukaista tilannetta. Merkitään funktioiden \(f(x)\) ja \(g(x)\) kuvaajien väliin jäävää pinta-alaa \(A\). Oletetaan, että \(f(x_1)=g(x_1)\) ja \(f(x_2)=g(x_2)\), eli funktioiden kuvaajan leikkaavat pisteissä \(x_1\) ja \(x_2\). Tällöin pinta-ala saadaan laskemalla:

\(A=\int_{x_1}^{x_2} f(x)~\text{d}x - \int_{x_1}^{x_2} g(x)~\text{d}x\)

Perusteluna laskukaavalle on:

• \(\int_{x_1}^{x_2} f(x)~\text{d}x\) määrittää funktion \(f(x)\) ja \(x\)-akselin väliin jäävän pinta-alan \(a\)

• \(\int_{x_1}^{x_2} g(x)~\text{d}x\) määrittää funktion \(g(x)\) ja \(x\)-akselin väliin jäävän pinta-alan \(b\)

• edellisten alueiden erotus on funktioiden \(f(x)\) ja \(g(x)\) väliin jäävä pinta-ala \(A=a-b\)

Käytännössä ensin joudutaan lasketaan, milloin \(f(x)=g(x)\) eli miten valitaan määrätyn integraalin rajat \(x_1\) ja \(x_2\).

Esimerkki

Laske funktioiden \(3x^2\) ja \(x+4\) kuvaajien väliin jäävä pinta-ala. Funktioiden kuvaajat on esitetty alla.

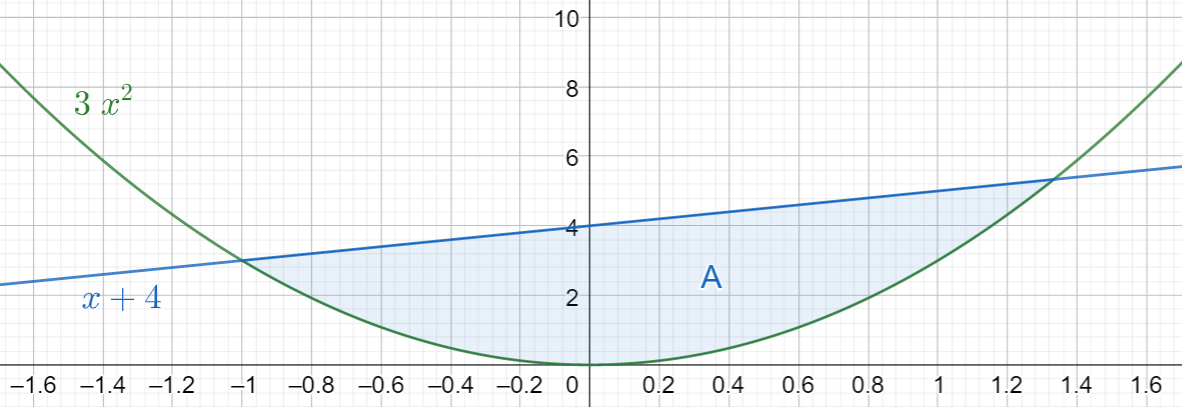
Ratkaisu

Koska leikkauspisteiden välissä pätee \(x+4 \geq 3x^2\), niin valitaan \(f(x)=x+4\) ja \(g(x)=3x^2\). Lasketaan, milloin funktioiden arvot ovat yhtä suuret, eli missä pisteissä niiden kuvaajat leikkaavat:

\(3x^2=x+4\)

\(3x^2-x-4=0\)

\(x=\frac{-(-1)\pm \sqrt{(-1)^2-4\cdot 3\cdot (-4)}}{2\cdot 3}\)

\(x=\frac{1\pm \sqrt{49}}{6}\)

\(x=\frac{1\pm 7}{6}\)

Leikkauspisteiksi saadaan \(x_1=\frac{1-7}{6}=-1\) ja \(x_2=\frac{1+7}{6}=\frac{4}{3}\).

Nyt voidaan laskea ala:

\(\begin{align} & A=\int_{-1}^{4/3} x+4~\text{d}x - \int_{-1}^{4/3} 3x^2~\text{d}x \\ & = \overset{4/3}{\underset{-1}{/}} \frac{1}{2}x^2+4x - \overset{4/3}{\underset{-1}{/}} x^3 \\ & = \left[\left(\frac{1}{2}\cdot \left(\frac{4}{3}\right)^2+4\cdot\frac{4}{3}\right) - \left(\frac{1}{2}\cdot(-1)^2+4\cdot (-1)\right) \right]\\ & - \left[\left(\frac{4}{3}\right)^3-(-1)^3\right]\\ & = \left(\frac{16}{18}+\frac{16}{3}\right)-\left(\frac{1}{2}-4\right)-\left(\frac{64}{27}+1\right) \\ & = \frac{343}{54} \end{align}\)

Kaaren pituus

Kaaren pituuden laskeminen liittyy varsinkin sellaisiin funktioihin, joiden kuvaaja ei ole suora. Esimerkiksi kahden kiinnityspisteen välillä roikkuvan köyden tai ketjun korkeutta maasta kuvaa ns. ketjukäyrä. Jos ketjukäyrän funktion lauseke tiedettäisiin, niin sen perusteella voitaisiin laskea ketjun pituus.

Funktion \(f(x)\) kuvaajan kaaren pituus \(s\) välillä \(x_1 \leq x \leq x_2\) saadaan kaavalla

\(s=\int_{x_1}^{x_2} \sqrt{1+[f'(x)]^2}~\text{d}x\)

Perustelu

Perusteluna voidaan käyttää seuraavaa kuvaa:

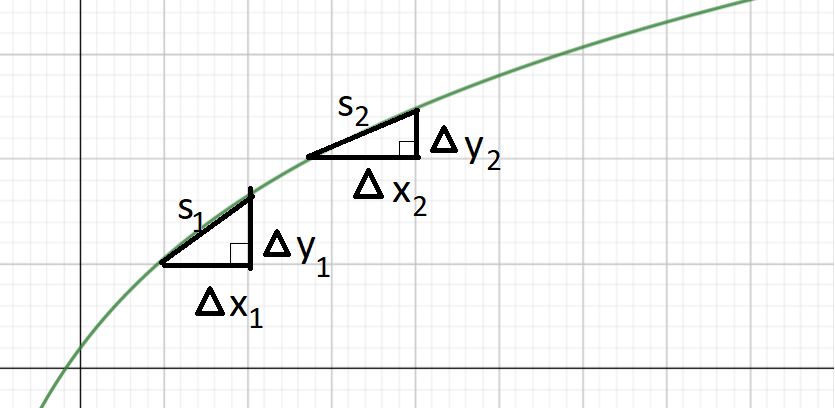
Kaaren pituus \(s\) jakautuu osapituuksiin \(s_1,s_2, \dots s_n\). Jokaisen osan pituutta \(s_i\) approksimoidaan suorakulmaisen kolmion hypotenuusalla, kun kolmion kateetit ovat \(\Delta x_i\) ja \(\Delta y_i\). Kateettien avulla ilmaistuna pituus on Pythagoraan lauseen mukaisesti \(s_i=\sqrt{(\Delta x)^2+(\Delta y)^2}\). Neliöjuuren sisällä oleva lauseke voidaan kirjoittaa myös seuraavassa muodossa:

\((\Delta x_i)^2+(\Delta y_i)^2=(\Delta x_i)^2 \left(1+\frac{(\Delta y_i)^2}{(\Delta x_i)^2}\right)\)

Karkea arvo koko kaaren pituudelle saadaan summana näistä pituuksista:

\(s\approx \Sigma_{i=1}^n \sqrt{(\Delta x_i)^2 \left(1+\frac{(\Delta y_i)^2}{(\Delta y_i)^2}\right)}\)

Varsinaisesti kaaren pituus saadaan raja-arvona, jossa kaari on jaettu äärettömään moneen osaan \(s_i\):

\(s=\lim_{n\to\infty} \Sigma_{i=1}^n \sqrt{(\Delta x_i)^2 \left(1+\frac{(\Delta y_i)^2}{(\Delta x_i)^2}\right)}\)

Osamäärä \(\frac{\Delta y_i}{\Delta x_i}\) on sama kuin \(f'(x)\), jos \(\Delta x\) lähenee nollaa. Näinhän käykin, kun osapituuksen \(s_i\) määrä lähenee ääretöntä. Edelleen integraalin määritelmän perusteella summa, jossa yhteenlaskettavia on äärettömän monta, voidaan esittää integraalina:

\(s=\int \sqrt{1+[f'(x)]^2}~\text{d}x\)

Tarkastellaan esimerkkinä kuvan mukaista jokea, joka ylhäältä päin näyttäisi funktion \(f(x)=e^{0.01x} \sin{(0.1x+4)}\) kuvaajalta. Minkä verran mutkittelu lisää joen pituutta kohtien \(x=0\) km ja \(x=150\) km välillä? (Tällaisia mutkittelevia eli ns. meanderoivia jokia on oikeasti olemassa. Niitä muodostuu, kun vedenvirtausnopeus joen eri rannoilla vaihtelee esimerkiksi hiekan kasautumisen takia. Oikeasti mutkittelu tietysti noudattaa monimutkaisempia funktioita.)

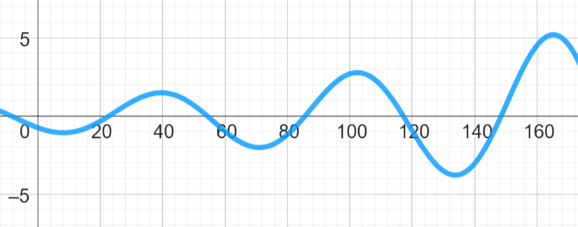
Joen pituuden laskuun tarvitaan derivaatta \(f'(x)\). Funktio \(f(x)\) on kahden yhdistetyn funktion tulo, joten derivaatan laskeminen ei ole ihan yksinkertaista. Lisäksi derivaatan lauseke pitää korottaa toiseen potenssiin ja integraalissa tarvitaan vielä neliöjuurtakin. Lasku on siis parasta suorittaa symbolisella laskimella. Välivaiheena voi ensin laskea derivaatan lausekkeen, joka tässä tapauksessa on \(f'(x)=e^{0.01 x}) (0.1 \cos{(4 + 0.1 x)} + 0.01 \sin{(4 + 0.1 x))}\). Sitten tämä lauseke sijoitetaan määrätyn integraalin laskukaavaan. Tämän esimerkin joen pituudeksi tulee noin 152.4 km, eli mutkittelu lisäsi pituutta noin 2.4 km. Joissakin laskimissa on myös mahdollista käyttää valmista komentoa esim. “length of curve” tai “arc length”.

Esimerkki

Laske funktiota \(f(x)=\frac{2}{3} x\sqrt{x}\) kuvaavan kaaren pituus välillä \(0 \leq x \leq 1\).

Ratkaisu

Kaaren pituuden laskukaavaan tarvitaan funktion \(f(x)\) derivaatta \(f'(x)\). Derivaatan laskua varten muutetaan funktio \(f(x)\) murtopotenssimuotoon:

\(f(x)= \frac{2}{3} x\cdot x^{1/2}= \frac{2}{3} x^{1+\frac{1}{2}}=\frac{2}{3} x^{\frac{3}{2}}\)

Derivaataksi saadaan nyt

\(f'(x)=\frac{2}{3}\cdot \frac{3}{2}x^{\frac{1}{2}}=x^{\frac{1}{2}}\)

Laskukaavaan tarvitaan derivaatan toinen potenssi:

\([f'(x)]^2=\left(x^{\frac{1}{2}}\right)^2=x\)

Sijoitetaan tämä kaaren pituuden laskukaavaan:

\(s=\int_0^1 \sqrt{1+x}~\text{d}x\)

Integraaliksi saadaan

\(\int \sqrt{1+x}~\text{d}x = \int (1+x)^{1/2}~\text{d}x = \frac{2}{3}(1+x)^{3/2}\)

Kaaren pituus on siis

\(s=\frac{2}{3} (1+1)^{3/2} - \frac{2}{3}(1+0)^{3/2} \approx 1.219\)

Esimerkki

Liikutaan käyrällä \(f(x)=3x+2\) aloittaen pisteestä \(x=1\). Mihin asti pitää edetä, että kuljettu matka on 20 yksikköä?

Ratkaisu

Merkitään päätepistettä vaikkapa kirjaimella \(a\). Lasketaan aluksi funktion derivaatta \(f'(x)=3\). Sijoitetaan se kaaren pituuden laskukaavaan ja sievennetään lauseke:

\(S=\int_1^a \sqrt{1+3^2}~\text{d}x = \int_1^a \sqrt{10}~\text{d}x = \overset{a}{\underset{1}{/}} \sqrt{10}x = \sqrt{10}a-\sqrt{10}\)

Ratkaistaan yhtälö vaaditulle matkan pituudelle:

\(\sqrt{10}a-\sqrt{10}=20\)

\(\sqrt{10}a=20+\sqrt{10}\)

\(a=\frac{20+\sqrt{10}}{\sqrt{10}}\approx 7.32\)

Tässä tapauksessa funktio on suora, joten tehtävän voisi useiden välivaiheiden kautta ratkaista myös suorakulmaisen kolmion laskukaavoilla.

Funktion keskiarvo

Funktion \(f(x)\) keskiarvo \(\overline{f}(x)\) arvojen \(x=a\) ja \(x=b\) välissä saadaan laskemalla:

\(\overline{f}(x)=\frac{1}{b-a} \int_a^b f(x)~\text{d}x\)

Perustelu

Perustellaan kaava seuraavasti:

• jaetaan väli \([a,b]\) yhtä suuriin paloihin, joita on \(n\) kappaletta

• jokaisen palan leveys on \(\Delta x = \frac{b-a}{n}\)

• palojen määrä \(n\) voidaan ilmasta välin päätepisteiden ja osien leveyden avulla \(n=\frac{b-a}{\Delta x}\)

• lasketaan funktiot arvot jokaisessa välin \([a,b]\) jakopisteessä \(x_1, x_2, \dots ,x_n\), arvot ovat siis \(f(x_1), f(x_2), \dots, f(x_n)\)

• funktion keskiarvo on tällöin

\(\overline{f}(x)=\frac{f(x_1)+f(x_2)+\dots+f(x_n)}{n} \)

Sijoittamalla \(n=\frac{b-a}{\Delta x}\) saadaan

\(\overline{f}(x)= \frac{f(x_1)+f(x_2)+\dots+f(x_n)}{\frac{b-a}{\Delta x}}\),

joka sievenee muotoon

\(\overline{f}(x)= \frac{\Delta x}{b-a} \left(f(x_1)+f(x_2)+\dots+f(x_n)\right) = \frac{\Delta x}{b-a} \Sigma_{i=1}^n f(x_i)\),

missä \(\Sigma_{i=1}^n f(x_i)\) on lyhennysmerkintä summalle \(f(x_1)+f(x_2)+\dots+f(x_n)\).

Mitä enemmän on osavälejä, sitä tarkemmin funktion keskiarvo saadaan laskettua. Ääritapauksena lasketaan raja-arvo, jossa \(n \to \infty\):

\(\overline{f}(x)=\lim_{n \to \infty} \frac{1}{b-a} \Delta x \Sigma_{i=1}^n f(x_i)\)

eli toisin kirjoitettuna

\(\overline{f}(x)= \frac{1}{b-a} \lim_{n \to \infty} \Sigma_{i=1}^n f(x_i) \Delta x\),

jossa loppuosa on sama kuin määrätyn integraalin määritelmä:

\(\overline{f}(x)= \frac{1}{b-a} \int_a^b f(x)~\text{d}x\).

Esimerkki

Laske funktion \(f(x)=3x^2+2x\) keskiarvo välillä \(1\leq x \leq 3\).

Ratkaisu

Funktion keskiarvo annetulla välillä on

\(\begin{align} \overline{f}(x) & = \frac{1}{3-1} \int_1^3 3x^2+2x~\text{d}x \\ & = \frac{1}{2} \left((3^3+3^2)-(1^3+1^2)\right) \\ & = \frac{1}{2} (27+9-1-1) = 17\end{align}\)

Neliöllinen ja tehollinen keskiarvo

Pistorasiasta saadaan Suomessa vaihtovirtaa 50 Hz taajuudella. Sähköjännitteen suuruus \(u\) ajanhetkellä \(t\) noudattaa kuvan mukaista funktiota \(u(t)=u_0 \sin{\omega t}\), missä \(u_0\) on jännitteen huippuarvo (yleensä 325 V) ja \(\omega\) on kulmataajuus \(2\pi\cdot 50\) (radiaania sekunnissa). Mikä on jännitteen suuruus keskimäärin?

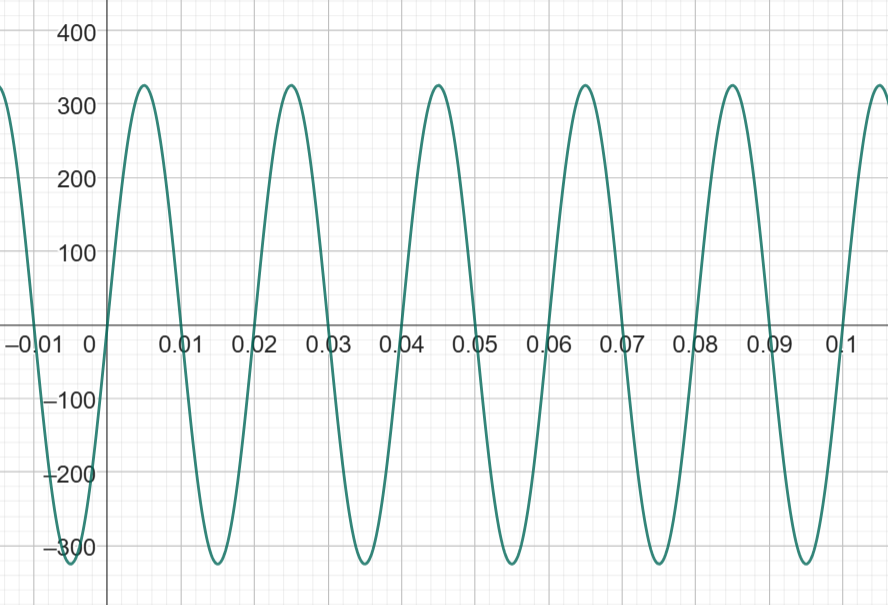
Keskiarvo suoraan kuvaajasta pääteltynä tai funktion lausekkeesta laskettuna olisi nolla volttia. Kuitenkin arkikokemuksen mukaisesti pistorasiasta tulee sähköä keskimäärin suuremmalla kuin nollan voltin jännitteellä. Tällaisessa tapauksessa lasketaan neliöllinen keskiarvo kaavalla

\(\overline{f}^2 = \frac{1}{b-a}\int_a^b \left(f(x)\right)^2~\text{d}x\)

ja sen jälkeen lasketaan vielä tehollinen keskiarvo, joka on neliöjuuri edellisen laskun tuloksesta.

Sähköjännitteen neliöllinen keskiarvo yhden jakson eli \(\frac{1}{50}=0.02\) sekunnin aikana on siis

\(\overline{u}^2 = \frac{1}{0.02-0}\int_0^{0.02} \left(325\cdot \sin{(2\pi \cdot 50 t)}\right)^2~\text{d}t\)

Lasku kannattaa suorittaa laskimella, jolloin saadaan neliöllisen keskiarvon lukuarvoksi 52812.5. Tehollinen jännite on \(\sqrt{52812.5}\) V eli 230 V.

Painopisteen laskeminen

Integraalilaskennassa painopiste lasketaan periaatteessa samalla tavalla, mutta kappale jaetaan äärettömän moneen osaan, joiden leveys lähenee nollaa. Tarkastellaan tässä vain tasoaluetta, jonka yläreunan rajaa funktio \(f(x)\) ja alareunan \(x\)-akseli. Reunoilla voivat olla suorat \(x=a\) ja \(x=b\) tai funktion \(f(x)\) nollakohdat. Painopiste on mahdollista laskea myös kahden funktion rajaamalle tasoalueelle, mutta siihen tarvittavia laskukaavoja ei käsitellä tässä materiaalissa.

Oletetaan, että tarkasteltava kappale on kuvan kaltainen, kauttaaltaan homogeeninen eli esimerkiksi vain yhdenlaisesta materiaalista valmistettu tasapaksu levy. Tällöin painopisteen laskukaavaan voi sijoittaa kappaleen osien massojen sijaan osien pinta-alat, sillä riippumatta siitä, onko materiaali esimerkiksi pahvia, betonia vai lunta, jokaisen osan massa on suoraan verrallinen osan pinta-alaan. Tällöin painopisteen laskukaavan osaa \(x_1 m_1 + x_2 m_2 + \dots\) vastaa integraali \(\int_a^b x\cdot f(x)~\text{d}x\). Kaavassa \(f(x)~\text{d}x\) vastaa äärettömän kapean suikaleen pinta-alaa (kuten määrätyn integraalin laskussakin) ja \(x\) kyseisen osan sijaintia.

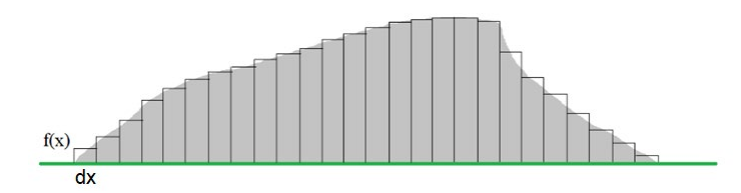
Painopisteen laskukaavan kohtaa \(m_1 + m_2 + \dots\) vastaa koko funktion kuvaajan rajaama pinta-ala, sillä koko kappaleen massa on suoraan verrannollinen kappaleen pinta-alaan. Massojen summan paikalle painopisteen laskukaavaan tulee siis määrätyn integraalin avulla laskettava pinta-ala\(A=\int_a^b f(x)~\text{d}x\). Laskukaavaksi muodostuu siis:

\(x_p=\frac{1}{A}\int_a^b x\cdot f(x)~\text{d}x\)

Painopisteelle voidaan määrittää myös \(y\)-koordinaatti \(y_p\). Tällöin ajatellaan, että pystysuunnassa jokaisen osan painopiste on puolivälissä kyseistä osaa, siis \(x\)-akselista mitattuna korkeudella \(\frac{1}{2} f(x)\). Tämä vain sijoitetaan edelliseen laskukaavan osan sijainnin \(x\) paikalle. Saadaan laskukaava:

\(y_p=\frac{1}{A}\int_a^b \frac{1}{2}f(x) \cdot f(x)~\text{d}x\) eli \(y_p=\frac{1}{A}\int_a^b \frac{1}{2} \left[f(x)\right]^2~\text{d}x\)

Esimerkki

Käyrä \(f(x)=2x^2\), \(x\)-akseli ja suorat \(x=3\) ja \(x=5\) rajaavat tasoalueen. Laske tasoalueen painopisteen koordinaatit.

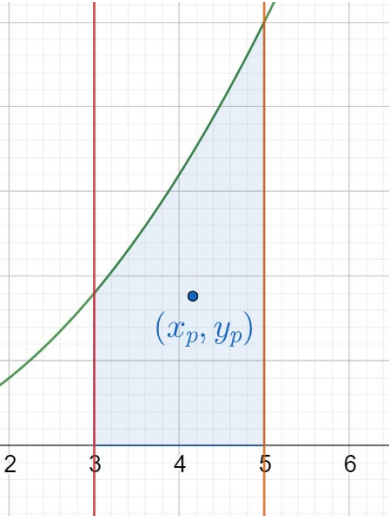
Ratkaisu

Lasketaan ensin pinta-ala \(A\), koska sitä tarvitaan kummankin koordinaatin laskemiseen.

\(A=\int_3^5 2x^2 ~\text{d}x = \overset{5}{\underset{3}{/}} \frac{2}{3}x^3 = \frac{2}{3}\cdot 5^3 - \frac{2}{3}\cdot 3^3 = \frac{196}{3}\approx 65.33\)

Koordinaatin \(x_p\) laskemiseen tarvitaan välivaihe:

\(\int_3^5 x\cdot 2x^2 ~\text{d}x = \overset{5}{\underset{3}{/}} \frac{1}{2}x^4 = \frac{1}{2}\cdot 5^4 - \frac{1}{2}\cdot 3^4 = 272\)

Koordinaatin \(y_p\) laskemiseen tarvitaan välivaihe:

\(\int_3^5 \frac{1}{2}\cdot (2x^2)^2 ~\text{d}x = \overset{5}{\underset{3}{/}} \frac{2}{5}x^5 = \frac{2}{5}\cdot 5^5 - \frac{2}{5}\cdot 3^5 = 1152.8\)

Painopisteen koordinaatit ovat siis \(x_p=\frac{272}{65.33}\approx 4.16\) ja \(y_p=\frac{1152.8}{65.33}\approx 17.64\).