Virheen arviointia

Aina, kun mitataan jotakin, tulokseen liittyy mittausvälineen epätarkkuudesta johtuva virhemarginaali. Usein mittaustuloksista lasketaan jokin kiinnostava suureen arvo. Esimerkiksi kun mitataan tynnyrin pohjan halkaisija ja tynnyrin korkeus, voidaan laskea tynnyrin tilavuus. Tilavuutta ei tällöin pitäisi ilmoittaa ehdottoman tarkkana arvona, vaan siten, että tuloksessa on huomioitu mittausten epätarkkuus. Virhe ei tässä yhteydessä tarkoita väärin tehtyä mittausta, vaan sitä, millä tarkkuudella mittavälineellä saa arvioitua suureen arvon.

Mittaustuloksia tai niistä laskettuja arvoja voidaan ilmoittaa käyttäen joko absoluuttista tai suhteellista virhettä. Ensimmäisessä menetelmässä virhemarginaalina ilmoitetaan mittauslaitteen tarkkuus, tai jos on käytetty useampia laitteita, niin niistä laskettu absoluuttinen virhe. Esimerkiksi jos virtamittarilla voi mitata virtaa 0.1 ampeerin tarkkuudella, niin silloin mittarilukema 2.4 ampeeria pitäisi ilmoittaa muodossa \(2.4~\text{A} \pm 0.1~\text{A}\) tai \((2.4\pm 0.1)~\text{A}\). Suhteellinen virhe taas tarkoittaa sitä, että lasketaan absoluuttista virhettä vastaava prosenttiosuus varsinaisesta mittaustuloksesta. Tällöin edellinen tulos olisi \(2.4~\text{A}\pm 8.4~\%\). (Absoluuttinen virhe 0.1 on 8.333… % luvusta 2.4, mutta hyvän tavan mukaista on pyöristää virhemarginaali ylöspäin.)

Tässä perehdytään virheen arviointiin kolmella eri tavalla:

• yhden muuttujan funktion virhe derivaatan avulla

• monen muuttujan funktion virhe osittaisderivaattojen avulla

• monen muuttujan funktion virhe suhteellisen virheen menetelmällä.

Millä tahansa menetelmällä virhe onkaan arvioitu, niin tuloksen ja virheen ilmoittamisessa voidaan käyttää seuraavia periaatteita:

• virhe ilmoitetaan yhden merkitsevän numeron tarkkuudella ja ylöspäin pyöristettynä

• tulos ilmoitetaan yhtä monella desimaalilla kuin virhekin normaaliin tapaan pyöristettynä

Näiden periaatteiden mukaan jos vaikkapa puutukin massaksi on laskettu \(72.94~\text{kg}\) ja virheeksi on tavalla tai toisella arvioitu \(0.34~\text{kg}\), niin virhe ilmoitettaisiin muodossa \(0.4~\text{kg}\) ja massa olisi tällöin virherajoineen \(72.9\pm 0.4~\text{kg}\). On kuitenkin olemassa muitakin sääntöjä suureiden arvon tarkkuudelle, kuten lähtöarvoissa käytettyjen merkitsevien numeroiden tai desimaalien määrä.

Yhden muuttujan funktion virhe

Kun funktio riippuu vain yhdestä muuttujasta eli on muotoa \(f(x)\), niin suureen arvolle voidaan määrittää virhemarginaali \(\Delta f = f'(x) \Delta x\), missä \(\Delta x\) on muuttujan \(x\) arvon määrittämisessä esiintyvä epätarkkuus.

Laskukaava perustuu niinsanottuun funktion differentiaaliin. Ajatus on sama kuin Newtonin menetelmässäkin: kun siirrytään pisteestä \(x\) pisteeseen \(x+\Delta x\), niin funktion arvoissa tapahtuu siirtymä pisteestä \(y(x)\) pisteeseen \(y(x+\Delta x)\). Funktion arvon muutosta voidaan merkitä lyhyemmin \(\Delta y = y(x+\Delta x)-y(x)\). Kun pisteet \(x\) ja \(x+\Delta x\) ovat lähellä toisiaan, niin funktion derivaatta \(y'(x)\) on suunnilleen sama kuin osamäärä \(\frac{\Delta y}{\Delta x}\) eli \(y'(x)\approx \frac{\Delta y}{\Delta x}\). Tätä sanotaan funktion differentiaaliksi.

Esimerkki

Kuinka suuri virhe aiheutuu, jos laskussa \(3.1^2\) käytetäänkin kantalukuna lukua \(3\)? Arvioi funktion differentiaalin avulla.

Ratkaisu

Laskua voidaan kuvata funktiolla \(f(x)=x^2\). Tämän funktion differentiaali on \(2x \Delta x\). Luvun \(x\) muutos on tässä \(\Delta x = 3-3.1=-0.1\). Sijoittamalla luvut differentiaaliin saadaan tulos \(2\cdot 3.1\cdot (-0.1) = -0.62\).

Todellinen virhe on \(y(3)-y(3.1)=3.1^2-3^2=9-9.61=-0.61\). Luku on melkein sama kuin yllä. Differentiaalia käytettäessä ei varsinaista laskutoimitusta \(x^2\) tarvinnut suorittaa ollenkaan.

Esimerkki

Laske ympyrän ala \(A\) ja sen virhemarginaali \(\Delta A\), kun ympyrän halkaisijaksi on mitattu \(d=3.22~\text{m}\) mittanauhalla, jonka tarkkuus on on \(\Delta d = 0.05~\text{m}\).

Ratkaisu

Ympyrän ala on \(A(d)=\frac{\pi}{4} d^2\). Funktion derivaatta on \(A'(d)=\frac{\pi}{2}d\).

Ympyrän alaksi saadaan \(A(3.22~\text{m})=\frac{\pi}{4} (3.22~\text{m})^2 = 8.14~\text{m}^2\).

Virhemarginaali on \(\Delta A = A'(3.22~\text{m})\cdot 0.05~\text{m}=\frac{\pi}{2} 3.22~\text{m} \cdot 0.05~\text{m} = 0.253~\text{m}^2\). Pyöristetään virhe ylöspäin yhden merkitsevän numeron tarkkuuteen: \(\Delta A = 0.3~\text{m}^2\).

Pinta-ala on siis absoluuttisen virheen avulla ilmoitettuna \(A=(8.1\pm 0.3)~\text{m}^2\).

Differentiaali yhtälössä

Differentiaalin käsite yhdistää muuttujan arvon muutoksen ja funktion arvon muutoksen. Siten differentiaalia voidaan käyttää myös muutoksen eikä virheen tai epätarkkuuden arviointiin.

Tarkastellaan esimerkkinä suoran ympyräpohjaisen kartion muotoista kasaa, jossa on kahvipapuja. Eri aineille on määritetty ns. kasautumiskulmia (angle of repose), jotka kuvaavat sitä, millainen on aineesta muodostuvan kasan kaltevuus. Kahvipavuille sivun jyrkkyytenä voidaan käyttää noin 40 astetta. Jos kasaan kaadetaan lisää kahvipapuja 2.0 kuutiometriä minuutissa, niin millä nopeudella kasan pohjaympyrän säde kasvaa?

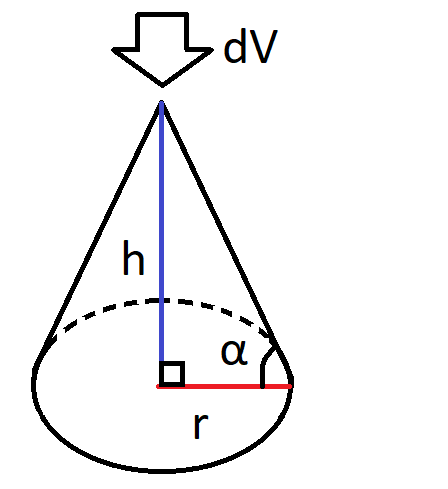
Muodostetaan ensin funktio kartion tilavuudelle \(V(r,h)\), jossa muuttujina ovat pohjan säde \(r\) ja kasan korkeus \(h\). Kartion tilavuus näiden avulla ilmaistuna on geometrian kaavojen perusteella \(V(r,h)=\frac{1}{3} \pi r^2 h\). Muutetaan tämä yhden muuttujan \(r\) funktioksi. Seinän jyrkkyydestä saadaan ehto \(\tan{\alpha}=\frac{h}{r}\), joten korkeus voidaan ilmaista muodossa \(h=r\tan{\alpha}\). Tilavuus on siis \(V(r)=\frac{1}{3} \pi r^2 \cdot r\tan{\alpha} = \frac{1}{3} \pi r^3 \tan{\alpha}\).

Kasan tilavuuden kasvunopeus on \(\Delta V\) ja toisaalta differentiaalin määritelmän mukaan \(V'(r)=\frac{\Delta V}{\Delta r}\). Tästä voidaan ratkaista \(\Delta r = \frac{\Delta V}{V'(r)}\). Tähän sijoitetaan \(V'(r)=\pi r^2 \tan{\alpha}\) ja ratkaistaan sitten yhtälöstä \(\Delta r\). Säteen muutosnopeus jollakin tietyllä säteen arvolla on siis

\(\Delta r = \frac{2~\text{m}^3/\text{min}}{\pi r^2 \tan{40^{\circ}}}\)

Esimerkiksi, jos kasan pohjan säde on 1 metri, niin se kasvaa nopeudella

\(\Delta r = \frac{2~\text{m}^3/\text{min}}{\pi \cdot (1~\text{m})^2 \tan{40^{\circ}}}\approx 0.76 ~\text{m/min}\)

ja kun kasan pohjan säde on 6 metriä, niin kasvunopeus on vain

\(\Delta r = \frac{2~\text{m}^3/\text{min}}{\pi \cdot (6~\text{m})^2 \tan{40^{\circ}}}\approx 0.02 ~\text{m/min}\).

Monen muuttujan funktion virhe

Jos funktio riippuu muuttujista \(x,y,z...\), niin tällöin funktion arvon suurin mahdollinen kokonaisvirhe riippuu yksittäisten muuttujien virheistä seuraavalla tavalla:

\(\Delta f \leq |\frac{\partial f}{\partial x}\Delta x| + |\frac{\partial f}{\partial y} \Delta y| + |\frac{\partial f}{\partial z} \Delta z| + ...\),

missä merkintä \(\frac{\partial f}{\partial x}\) tarkoittaa funktion \(f(x,y,z,...)\) derivaattaa ainoastaan muuttujan \(x\) suhteen, eli osittaisderivaattaa (vastaavasti määritellään muut osittaisderivaatat). Virheen laskukaava rakentuu samalla tavalla eri muuttujien differentiaalien avulla kuin yhden muuttujan funktion virhe, ja laskukaavaa sanotaankin kokonaisdifferentiaaliksi. Kun funktiot ovat mitattujen suureiden (esimerkiksi aika, matka, massa) perusteella määritettyjä johdannaissuureita (esimerkiksi nopeus, tilavuus, tiheys), niin laskuissa kannattaa pitää mukana mitattujen suureiden yksiköitä. Virheen yksikön pitää nimittäin olla saman kuin lasketun suureenkin yksikön.

Virheen arvioinnin kaavassa virhe on siis enintään epäyhtälön oikean puoleinen suuruinen. Yksittäisten muuttujien virheistä otetaan laskuun itseisarvot, jotta negatiiviset ja positiiviset virheet eivät kumoaisi toisiaan. Tässä oletetaan, että muuttujat ovat toisistaan täysin riippumattomia, eli esimerkiksi kellon epätarkkuus ei vaikuta mittanauhan epätarkkuuteen

Käytännössä usein käytetään ns. virheen kasautumislakia, jossa osittaisvirheet korotetaan toiseen potenssiin ja niistä lasketaan summa ja sitten lopuksi otetaan neliöjuuri summasta. Toiseen potenssiin korotuksella on tässä sama merkitys kuin edellisessä kaavoissa itseisarvolla, eli negatiiviset ja positiiviset virheet eivät saa kumota toisiaan. Virheen kasautumislain mukaisesti kokonaisvirhe on siis

\(\Delta f = \sqrt{\left(\frac{\partial f}{\partial x} \Delta x \right)^2 + \left(\frac{\partial f}{\partial y} \Delta y\right)^2 + \left(\frac{\partial f}{\partial z} \Delta z \right)^2 + \dots}\)

Esimerkki

Määritä tynnyrin tilavuus virhemarginaaleineen (suurin mahdollinen virhe), kun tynnyrin pohjan halkaisija on \(d=(1.2 \pm 0.1)~\text{m}\) ja tynnyrin korkeus on \(h=(1.40\pm 0.05)~\text{m}\).

Ratkaisu

Tynnyrin tilavuus on \(V(d,h)=\frac{\pi}{4}d^2 h\).

Osittaisderivaatta halkaisijan suhteen on \(\frac{\partial V}{\partial d}=\frac{\pi}{2}dh\), josta saadaan osittaisvirheeksi

\(\frac{\pi}{2}\cdot 1.2~\cdot 1.40~\cdot 0.1 \text{m}^3 = 0.264~\text{m}^3\).

Osittaisderivaatta korkeuden suhteen on

\(\frac{\partial V}{\partial h}=\frac{\pi}{4}d^2\), josta saadaan osittaisvirheeksi

\(\frac{\pi}{4} \cdot 1.2^2 \cdot 0.05~\text{m}^3 = 0.057~\text{m}^3\).

Tilavuus on \(V(1.2~\text{m},1.4~\text{m})=\frac{\pi}{4} \cdot 1.2^2 \cdot 1.40 ~\text{m}^3 = 1.583~\text{m}^3\), ja virhemarginaali on

\(\Delta f \leq 0.264~\text{m}^3+0.057~\text{m}^3 = 0.317~\text{m}^3 \approx 0.4~\text{m}^3\).

Tynnyrin tilavuus on siis noin \((1.6 \pm 0.4)~\text{m}^3\).

Esimerkki

Tietyn muotoisille pyöriville tai vieriville kappaleille voidaan laskea hitausmomentti \(J\), joka on tarpeellinen suure esimerkiksi vauhtipyöriin liittyvissä sovelluksissa. Umpinaiselle pallolle, esimerkiksi keilapallolle, hitausmomentin saa kaavalla \(J=\frac{2}{5}mr^2\), missä \(m\) on pallon massa ja \(r\) säde. (Keilapallo on toki tähän huono esimerkki, koska se ei ole täysin homogeeninen, vaan siinä on kolot sormille.) Laske pallon hitausmomentti ja yläraja sen virheelle, kun massa 10.4 kg on mitattu 0.1 kg tarkkuudella, ja säde 0.27 m on mitattu 0.01 m tarkkuudella. Kumman mittavälineen virhe vaikuttaa hitausmomentin virheeseen enemmän?

Ratkaisu

Lasketaan ensin hitausmomentti: \(J=\frac{2}{5}\cdot 10.4~\text{kg}\cdot (0.27~\text{m})^2 = 0.303~\text{kgm}^2\)

Osittaisderivaatat ovat \(\frac{\partial J}{\partial m}=\frac{2}{5}r^2\) ja \(\frac{\partial J}{\partial r}=\frac{2}{5}m\cdot 2r=\frac{4}{5}mr\). Sijoittamalla mitatut suureet ja niiden virheet saadaan:

\(\Delta J = \frac{2}{5}\cdot (0.27~\text{m})^2\cdot 0.1~\text{kg} + \frac{4}{5}\cdot 10.4~\text{kg}\cdot 0.27~\text{m}\cdot 0.01~\text{m}\)

Ensimmäisestä termistä eli massan mittauksen epätarkkuudesta aiheutuu noin \(0.002916~\text{kgm}^2\) epätarkkuus, ja toisesta termistä eli säteen mittauksen epätarkkuudesta aiheutuu noin \(0.022464~\text{kgm}^2\) epätarkkuus. Kokonaisuudessaan hitausmomentin epätarkkuus on näiden summa.

Suhteellisen virheen menetelmä

Seuraavaksi tarkasteltava suhteellisen virheen menetelmä on helppo tapa arvioida monen muuttujan funktioiden virhettä. Se kuitenkin sopii vain sellaisille funktioille, joiden lauseke muodostuu muuttujien potenssien tuloista tai osamääristä, mahdollisesti vakiolla kerrottuna. Yleisesti kolmen muuttujan \(x,y,z\) funktion lauseke olisi tällöin \(f(x,y,z)=ax^m y^n z^k\), missä \(a,m,n,k\neq 0\). Esimerkki tällaisesta funktiosta on \(f(x,y,z)=2\frac{x^2 y^3} {z}\) eli \(f(x,y,z)=2 x^2 y^3 z^{-1}\).

Suhteellisen virheen laskukaava voidaan johtaa tulon ja osamäärän derivaattakaavojen perusteella. Suhteellisen virheen ylärajaksi saadaan muuttujien suhteellisten virheiden summa, jossa yhteenlaskettavat on painotettu muuttujien potenssien itseisarvoilla:

\(\frac{\Delta f}{f} \leq |n| \frac{\Delta x}{x} + |m| \frac{\Delta y}{y} + |k| \frac{\Delta z}{z}\)

Suhteellinen virhe voidaan lopuksi muuttaa absoluuttiseksi virheeksi siten, että laskettu tulos kerrotaan suhteellista virhettä vastaavalla osuudella.

Esimerkki

Varaston lattialla on hiekkaa ympyrän muotoisella alueella, jonka säteeksi arvioidaan 1.5 m. Säteen epätarkkuudeksi arvioidaan 0.2 m. Hiekkakerroksen paksuudeksi arvioidaan noin 0.3 m siten, että epätarkkuus on 0.05 m. Kuinka paljon hiekkaa on mittausten perusteella?

Ratkaisu

Hiekka muodostaa ympyräpohjaisen suoran lieriön, jonka tilavuus on \(V=\pi r^2 h\). Mitat ovat \(r=(1.5\pm 0.2)\) m ja \(h=(0.3\pm 0.05)\) m.

Tilavuudeksi saadaan \(V=\pi \cdot(1.5~\text{m})^2\cdot (0.3~\text{m}) = 2.1206~\text{m}^3\)

Virheen yläraja on \(\frac{\Delta V}{V} = 2\frac{\Delta r}{r}+\frac{\Delta h}{h} = 2 \frac{0.2}{1.5}+\frac{0.05}{0.3} = 0.433\)

Absoluuttinen virhe on \(0.433\cdot 2.1206~\text{m}^3 = 0.9182~\text{m}^3\)

Hiekan tilavuudeksi voidaan siis näiden mittausten perusteella arvioida \(V=(2.12 \pm 0.92)~\text{m}^3\)

Sivun alussa esitettyjen periaatteiden mukaisesti virhe olisi yhden merkitsevän numeron tarkkuudella \(1~\text{m}^3\), ja tällöin tilavuuskin pitäisi ilmaista vain kuutiometrin tarkkuudella: siis \(V=(2\pm 1)~\text{m}^3\).