Pyörähdyskappaleet

Tarkastellaan vielä erityistapauksena määrätyn integraalin sovelluksista pyörähdyskappaleen tilavuutta ja pinta-alaa. Pyörähdyskappale on jokin kolmiulotteinen muoto, joka on saatu aikaan siten, että jonkin funktion kuvaaja pyörähtää \(x\)-akselin ympäri. Funktion kuvaaja muodostaa siten kappaleen seinät.

Tilavuus

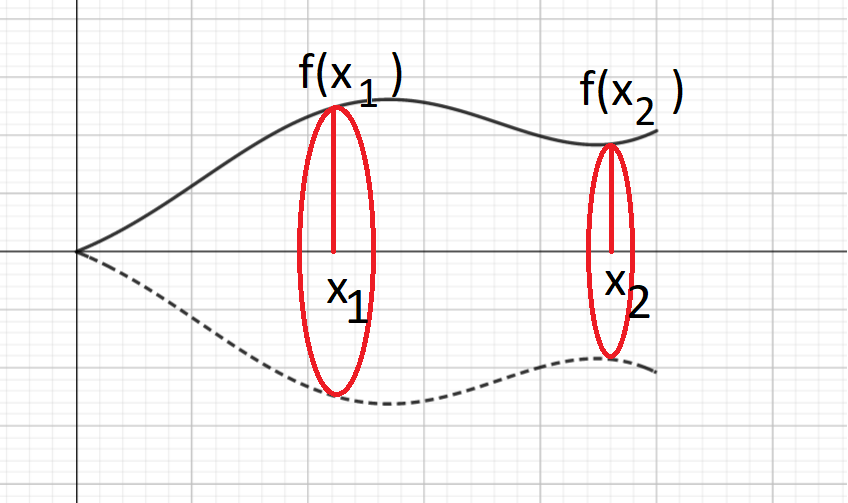
Kun funktion kuvaaja pyörähtää \(x\)-akselin ympäri, niin joka kohtaan muodostuu ympyrä, jonka säde on funktion arvo \(f(x)\). Oheisessa kuvassa on esitetty pyörähdyskappaleen poikkileikkaukset kohdissa \(x_1\) ja \(x_2\). Kohdassa \(x_1\) poikkileikkausta vastaavan ympyrän säde on \(f(x_1)\), kohdassa \(x_2\) poikkileikkausta vastaavan ympyrän säde on \(f(x_2)\). Yleisesti pisteessä \(x_i\) ympyrän pinta-ala on \(A_i=\pi f(x_i)^2\).

Oletetaan, että kappaleen seinämät muodostava funktio alkaa pisteestä \(x=a\) ja päättyy pisteeseen \(x=b\). Kun lasketaan koko pyörähdyskappaleen tilavuutta \(V\), niin kappale jaetaan äärettömän moneen, äärettömän ohueen viipaleeseen. Jokaisen viipaleen pinta-ala vastaa ympyrää, jonka säde on funktion arvo tietyssä pisteessä. Jokaisen ympyrän paksuudeksi ajatellaan hyvin pieni muutos vaaka-akselilla, \(\text{d}x\). Äärettömän monta kappaletta äärettömän ohuita viipaleita saadaan laskemalla integraali:

\(\int_a^b \pi f(x)^2~\text{d}x\)

Esimerkki

On kaadettu iso puu, jonka poikkileikkaus on ympyrä. Puu on tyvestä leveämpi ja latvasta ohuempi. Rungon sädettä (yksikössä cm) korkeudella \(x\) tyvestä mitattuna voidaan kuvata funktiolla \(f(x)=10-0.01x\) eli säde on alhaalla 10 cm ja pienenee aina metrin matkalla 1 cm. Mikä on puunrungon tilavuus tyvestä 300 cm korkeudelle?

Piirrä funktio vaikkapa GeoGebralla. Kuvaajassa puu on maassa kyljellään, ja \(x\)-akseli kulkee sen läpi rungon keskellä pituussuunnassa.

Ratkaisu

Jos runko sahattaisiin likimain tasapaksuiksi kiekoiksi, niin voitaisiin määrittää jokaisen kiekon tilavuus siten, että mitataan jokaisen kiekon säde \(f(x)\) ja paksuus \(\Delta x\) ja sitten lasketaan \(\pi [f(x)]^2 \Delta x\). Sitten laskettaisiin kiekkojen tilavuudet yhteen. Tarkan tilavuuden määrittämiseksi tarvittaisiin äärettömän monta, äärettömän ohutta kiekkoa eli käytännössä kasa sahanpurua. Integraalilaskennalla tilavuuden \(V\) määritys on helpompaa:

\(V=\int_0^{300} \pi (10-0.01x)^2~\text{d}x = 68801\) (yksikkönä cm\(^3\), eli 0.07 m\(^3\))

Puiden tilavuuksia määritetään metsäalalla eri menetelmillä kuin tällä, esimerkiksi tilavuusyhtälöiden avulla. Metsäkoneet voivat laskea puun tilavuutta paikan päällä esimerkiksi mittaamalla rungon halkaisijan muutaman senttimetrin välein ja käsitelemällä näitä pätkiä katkaistun kartion laskukaavoilla.

Esimerkki

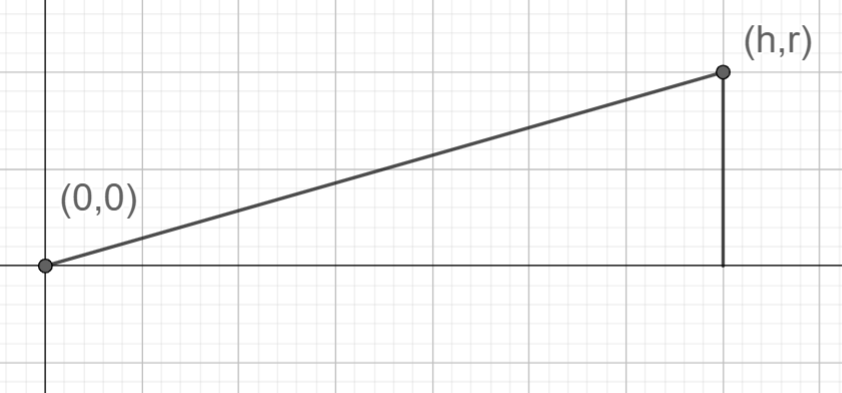
Kartion tilavuuden laskukaava on \(V=\frac{1}{3} \pi r^2 h\), missä \(r\) on kartion pohjaympyrän säde ja \(h\) on kartion korkeus. Johda tilavuuden laskukaava integroimalla. Kuvassa on esitetty kartion seinämän muodostavan funktion kuvaaja. Kartio on kyljellään siten, että sen kärki on pisteessä (0,0).

Ratkaisu

Muodostetaan ensin funktion \(f(x)\) lauseke. Kartion seinämän etäisyyttä kartion korkeusjanasta (kuvaajan \(x\)-akselista) kuvaa suora muotoa \(y=ax+b\). Koska kärki on origossa, niin leikkausvakio on \(b=0\). Kulmakertoimeksi saadaan

\(a=\frac{r-0}{h-0}=\frac{r}{h}\).

Funktio on siis \(f(x)=\frac{r}{h}x\), ja tilavuuden laskukaavassa tarvittava \(f(x)^2=\frac{r^2}{h^2}x^2\).

Lasketaan määrätty integraali pisteestä \(x=0\) pisteeseen \(x=h\):

\(\begin{align} V & = \int_0^h \pi \frac{r^2}{h^2}x^2~\text{d} x = \pi \frac{r^2}{h^2} \int_0^h x^2~\text{d}x \\ & = \pi \frac{r^2}{h^2} \left(\frac{1}{3}h^3-\frac{1}{3} 0^3 \right) \\ & = \pi \frac{r^2}{h^2} \cdot \frac{1}{3} h^3 = \frac{1}{3} \pi r^2 h \end{align}\)

Esimerkki

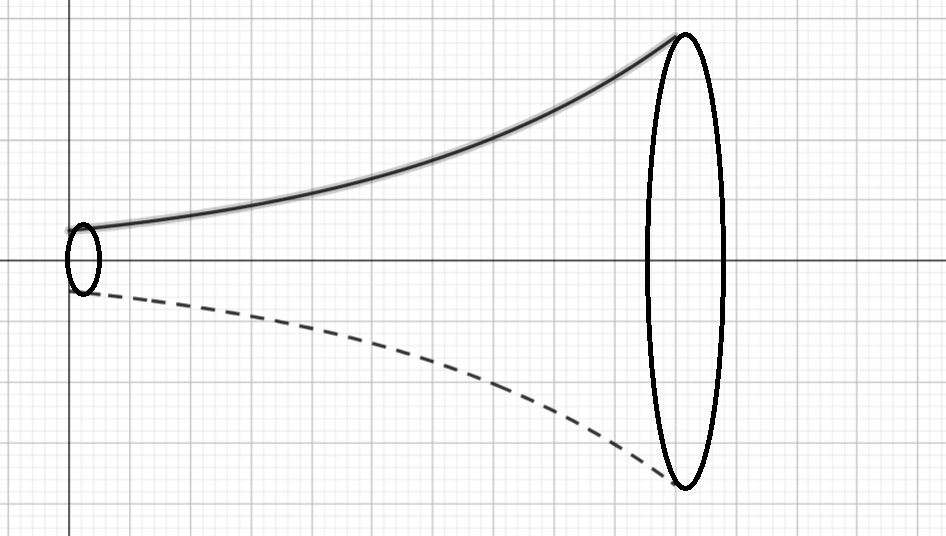
Laske pyörähdyskappaleen tilavuus, kun sitä rajoittaa käyrä \(f(x)=e^x\) välillä \(0 \leq x \leq 2\).

Ratkaisu

\(\begin{align} V & = \int_0^2 \pi (e^x)^2~\text{d}x \\ & = \pi \int_0^2 e^{2x}~\text{d}x \\ & = \pi \cdot \left( \frac{1}{2}e^{2\cdot 2} - \frac{1}{2} e^{2\cdot 0} \right) \\ & = \frac{\pi}{2} (e^4-e^0) = \frac{\pi}{2} (e^4-1) \approx 84.2 \end{align}\)

Pinta-ala

Pyörähdyskappaleen pinta-ala lasketaan samalla periaatteella kuin tilavuus: jakamalla kappale äärettömän moneen, hyvien ohueeseen kiekkoon, joiden säteet ovat funktion arvoja. Pinta-alan ajatellaan siis muodostuvan äärettömän monesta hyvin kapeasta “vyöstä”, jotka kiertävät pyörähdyskappaleen ympäri.

Kun pyörähdyskappaletta rajoittaa funktio \(f(x)\) välillä \(x_1 \leq x \leq x_2\), niin pyörähdyskappaleen pinta-ala on

\(A=2\pi \int_{x_1}^{x_2} |f(x)|\sqrt{1+[f'(x)]^2}~\text{d}x\)