Tasapainoehdot

Tarkastellaan jäykän kappaleen tasapainossa pysymistä. Jäykkiä kappaleita ovat esimerkiksi sillat, työkoneiden puomit ja vastaavat, sekä vaikkapa ihmisen raajat. Tasapainoehtojen avulla voi arvioida, millaisia voimia niveliin ja lihaksiin kohdistuu kun kädessä pidetään jotain painavaa esinettä.

Yleensä, kun lasketaan kappaleeseen vaikuttavia voimia, oletetaan että kappale on tasapainossa. Tällöin yhtälöt, joilla tehtävän ratkaisu onnistuu, saadaan ns. jäykän kappaleen tasapainoehdoista:

• kappaleeseen vaikuttavien voimien summa on nolla (= ei kiihtyvyyttä)

• kappaleeseen vaikuttavien momenttien summa on nolla (= ei kulmakiihtyvyyttä)

Tasapainoehtoisin liittyvissä laskuissa tarkastellaan usein erilaisiin liitoskohtiin tai tukiin liittyviä voimia. Laskut sujuvat helposti, kun ensin piirretään kuva systeemistä. Kuvaan pitäisi lisätä kaikki oleelliset voimat.

Sitten täytyy valita piste, jonka suhteen voimien momentteja lasketaan. Eräs helppo tapa on valita tämä momenttiakselipiste jonkin voiman kohdalle. Silloin nimittäin yhden voiman momentiksi saadaan nolla, ja lasku helpottuu. Pisteen voi kuitenkin valita vapaasti, esimerkiksi sillan tai palkin päädyn kohdalta.

Voimat kannattaa kirjoittaa allekkain taulukoksi. Taulukkoon voidaan kirjoittaa kaikkien voimien etäisyydet kyseisestä pisteestä. Siten taulukkoon saa helposti myös voimien momentit. Lopuksi kerätään taulukosta yhdeksi yhtälöksi voimien summa, ja toiseksi yhtälöksi momenttien summa, ja ratkaistaan tämä yhtälöpari.

Esimerkki

Metallinen palkki on 240 cm pitkä ja sen massa on 25 kg. Palkki lepää kahden tuen varassa siten, että toinen tuki (voima \(N_1\)) sijaitsee 10 cm palkin päädystä ja toinen tuki (voima \(N_2\)) sijaitsee 30 cm palkin vastakkaisesta päädystä. Laske tukivoimat \(N_1\) ja \(N_2\). Kuvaan on merkitty painovoima \(G=mg\) sekä tukivoimat \(N_1\) ja \(N_2\).

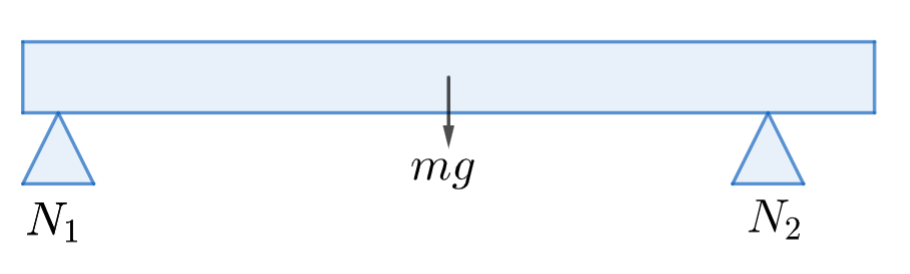
Ratkaisu

Lasketaan momentit voimasta \(N_1\) mitattuna. Ainoa tunnettu voima on \(G = mg= -25~\text{kg}\cdot 9.81~\frac{\text{m}}{\text{s}^2} = -245.25~\text{N}\). Tämän voiman etäisyys voimasta \(N_1\) on 1.1 m. Palkin painopistehän on puolivälissä palkkia eli 1.2 m palkin päädystä, mutta voima \(N_1\) on 10 cm päädystä oikealle.

Voiman \(N_2\) etäisyys on 2.0 m voimasta \(N_1\). Etäisyys saadaan laskemalla 2.40 m - 0.10 m - 0.30 m.

Kerätään voimat ja momentit taulukoon. Momenteista täytyy muistaa tarkistaa merkki. Voima \(G\) palkkia myötäpäivään ja \(N_2\) vastapäivään.

Voima (N)	Voiman varsi (m)	Momentti (Nm)
\(N_1\)	\(0\)	\(0\)
\(G=-245.25\)	\(1.1\)	\(-245.25\cdot 1.1 = -266.475\)
\(N_2\)	\(2.0\)	\(2N_2\)

Kootaan taulukon 1. sarakkeesta yhtälö, jonka mukaan voimien summa on nolla:

\(N_1-245.25 ~\text{N} +N_2=0\)

Taulukon 3. sarakkeesta saadaan yhtälö, jonka mukaan momenttien summa on nolla:

\(0-266.475 ~\text{N} +2 N_2 = 0\)

Jälkimmäisestä yhtälöstä voidaan ratkaista

\(N_2 = \frac{266.475~\text{N}}{2}=133.24~\text{N}\),

ja kun se sijoitaan ensimmäiseen yhtälöön, saadaan

\(N_1=245.25~\text{N}-133.24~\text{N}=112.01~\text{N}\),

eli voimat ovat noin 133 N ja 112 N.

WolframAlphalla ratkaisu saataisiin komennolla: N1-25*9.81+N2=0, -25*9.81*1.1+2*N2=0 (ratkaisut ovat hieman erilaisia lukuarvoiltaan, kun painovoima lasketaan suoraan yhtälöissä ilman välitulosta)

Esimerkki

Palkki on 300 cm pitkä ja painaa 10 kg. Palkin päällä 200 cm kohdalla on punnus, jonka massa on 5 kg. Laske tukivoimat \(N_1\) ja \(N_2\), kun ensimmäinen tuki (voima \(N_1\)) on aivan palkin päädyssä ja toinen tuki (voima \(N_2\)) 20 cm palkin toisesta päädystä.

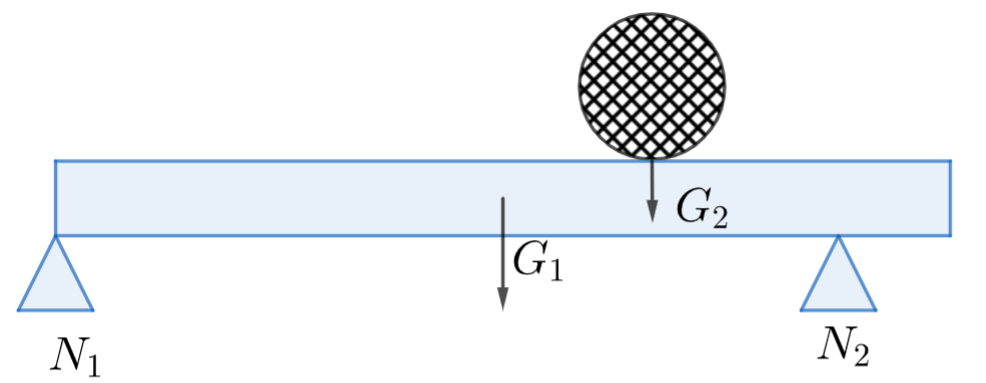
Ratkaisu

Valitaan momenttiakselipisteeksi voima \(N_1\). Nyt mukana on tukivoimien lisäksi palkin oma paino \(G_1\) ja punnuksen paino \(G_2\). Näiden suuruudet ovat

\(G_1 = -10~\text{kg}\cdot 9.81~\frac{\text{m}}{\text{s}^2} = -98.1~\text{N}\) ja \(G_2 = -5~\text{kg}\cdot 9.81~\frac{\text{m}}{\text{s}^2} = -49.05~\text{N}\) ja sijainnit vastaavasti 1.5 m (palkin painopiste on puolivälissä palkkia) ja 2.8 m (300 cm - 20 cm).

Kerätään voimat, etäisyydet ja momentit taulukkoon:

Voima (N)	Voiman varsi (m)	Momentti (Nm)
\(N_1\)	\(0\)	\(0\)
\(G_1=-98.1\)	\(1.5\)	\(-98.15\cdot 1.5 = -147.15\)
\(G_2 = -49.05\)	\(2.0\)	\(-49.05\cdot 2.0 = -98.1\)
\(N_2\)	\(2.8\)	\(2.8N_2\)

Voimayhtälö: \(N_1-98.1~\text{N}-49.05~\text{N}+N_2=0\)

Momenttiyhtälö: \(-147.15~\text{N}-98.1~\text{N}+2.8 N_2=0\)

Momenttiyhtälöstä saadaan \(N_2=\frac{147.15~\text{N}+98.1~\text{N}}{2.8}=87.59~\text{N}\)

ja edelleen voimayhtälöstä

\(N_1=98.1~\text{N}+49.05~\text{N}-87.59~\text{N}=59.56~\text{N}\).

WolframAlphalla ratkaisun saa komennolla:

solve N1-10*9.81-5*9.81+N2=0, -10*9.81*1.5-5*9.81*2+2.8*N2=0