Jatkuvat jakaumat

Jatkuvissa todennäköisyysjakaumissa muuttuja voi saada hyvin paljon erilaisia arvoja, joita on vaikea erotella selkeästi toisistaan. Tällaisia muuttujia voivat olla esim. paino, pituus, aika, lämpötila jne.

Jatkuvan jakauman todennäköisyysfunktio \(f(x)\) ei koostu erillisistä pylväistä kuten diskreetin jakauman todennäköisyysfunktio, vaan sen kuvaaja on jatkuva. Funktion avulla tapahtumien todennäköisyyksiä lasketaan kuvaajan ja \(x\)-akselin rajoittaman alueen pinta-alana. Pinta-alat lasketaan integroimalla. Taulukkolaskentaohjelmissa on valmiit funktiot jatkuvien jakamien käsittelyyn.

Tiheysfunktio voi olla matemaattiselta muodoltaan periaatteessa millainen tahansa, mutta sen pitää toteuttaa seuraavat ehdot:

1. \(f(x) \geq 0\) kaikilla arvoilla \(x\), sillä minkään tapahtuman todennäköisyys ei voi olla pienempi kuin 0

2. \(\int_{-\infty}^{\infty} f(x)~\text{d}x=1\), eli funktion kuvaajan ja \(x\)-akselin väliin jäävä pinta-ala on 1, sillä kaikkien mahdollisten tapahtumien todennäköisyydet ovat yhteensä 1. Kuvassa on esimerkki hyvin yksinkertaisesta funktiosta, joka toteuttaa annetut ehdot ja siten voi olla todennäköisyysjakauma.

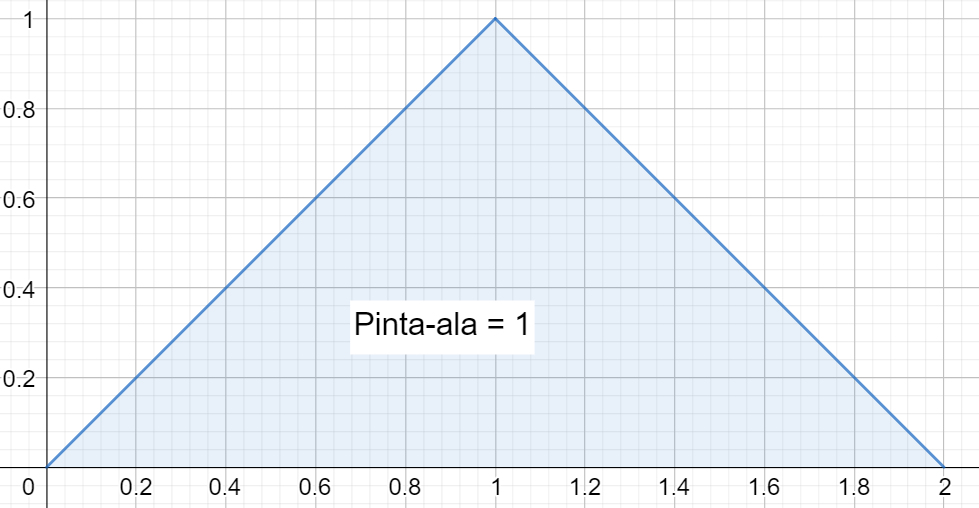
Jatkuvissa jakaumissa yksittäisen arvon todennäköisyys on nolla, koska sitä vastaava pinta-ala on nolla. Todennäköisyys sille, että satunnaismuuttuja \(X\) saa arvon \(x\), on korvattava todennäköisyydellä

\(P(x-\Delta x \leq X \leq x + \Delta x)\)

missä \(\Delta x\) on jokin virhemarginaali. Tällaisille laskuille ei usein ole tarvettakaan.

Kertymäfunktio \(F(x)\) antaa todennäköisyyden muuttujan arvoille, jotka ovat välillä \((-\infty, x)\). Tarkastellaan ylläolevaa todennäköisyysjakaumaa vastaavaa kertymäfunktiota. Esimerkiksi kertymäfunktion arvo \(F(0.4)\) tarkoittaa pinta-alaa siitä osasta kolmiota, joka jää kohdan \(x=0.4\) vasemmalle puolelle. Pinta-alaksi saadaan laskettua

\(F(0.4)=\frac{1}{2}\cdot 0.4 \cdot 0.4 = 0.08\).

Kertymäfunktion arvo \(F(1.4)\) saataisiin laskemalla \(x\)-akselin, käyrän ja kohdan \(x=1.4\) välille jäävän monikulmion pinta-ala. Se saadaan esimerkiksi laskemalla yhteen pisteillä merkityn kolmion ala \(0.5\) ja viivoilla merkityn puolisuunnikkaan ala \(0.32\). Siis \(F(1.4)=0.82\).

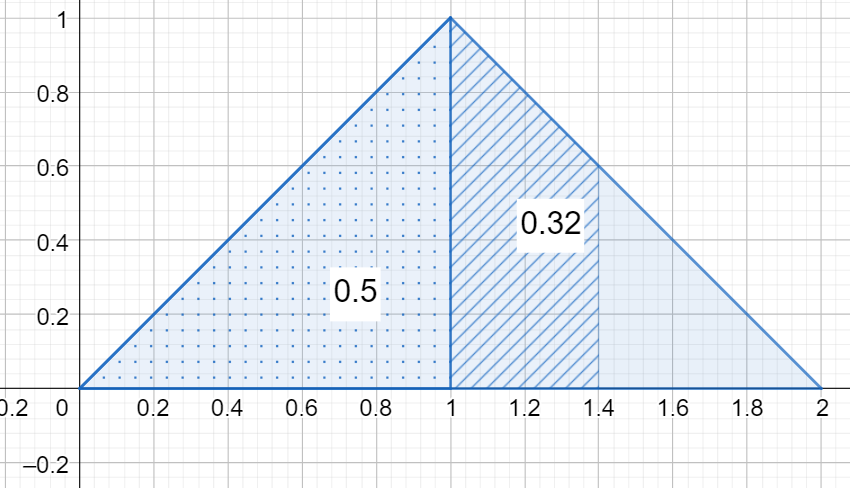
Kun pinta-aloja laskettaisiin eri \(x\):n arvoilla hyvin tiheästi, niistä voitaisiin piirtää alla oleva kuvaaja. Kuvaaja esittää siis esimerkkinä olevan todennäköisyysjakauman kertymäfunktiota.

Yleisesti kertymäfunktion arvo on todennäköisyysfunktion määrätty integraali, eli pinta-ala kuvaajan ja \(x\)-akselin välistä laskettuna äärettömän kaukaa vasemmalta muuttujan arvoon \(x\) asti. Kertymäfunktion viimeisen arvon pitää aina olla 1, sillä todennäköisyys sille, että satunnaismuuttuja saa suurimman mahdollisen tai jonkun sitä pienemmän arvon, on varmasti 1.

Odotusarvo \(\mu\) lasketaan integroimalla \(\mu = \int_{-\infty}^{\infty} x f(x)~\text{d}x\).

Varianssi on \(\sigma^2=\int_{-\infty}^{\infty} (x-\mu)^2 f(x)~\text{d}x\) ja keskihajonta on \(\sigma=\sqrt{\sigma^2}\).

Edellä mainittuja integraalilaskuja ei tarvitse laskea itse. Excelissä on tarvittavat funktiot.

Kertymäfunktion F(x) avulla lasketaan todennäköisyyksiä sille, että satunnaismuuttuja x on jollakin tietyllä välillä:

\(P(x\leq b)=F(b)\), \(P(x > b)=1-F(b)\), \(P(a < x < b)=F(b)-F(a)\)

Periaate on sama kuin diskreettien jakaumien tapauksessa. Funktio antaa suoraan todennäköisyyden sille, että muuttujan arvo on enintään määrätyn arvon verran. Todennäköisyys sille, että arvo on enemmän kuin parametriksi annettu arvo, on edellisen tapahtuman komplementti.

Graafisesti tarkasteltuna \(P(x \leq b)\) on alla olevan kuvan käyrän ja vaaka-akselin väliin jäävä raidoitettu osa, ja P\((x>b)\) on käyrän ja vaaka-akselin väliin jäävä valkoinen osa. Koska käyrän ja vaaka-akselin väliin jäävä pinta-ala oli tiheysfunktion määritelmän mukaan tasan 1, niin \(P(x>b)=1-P(x\leq b)=1-F(b)\).

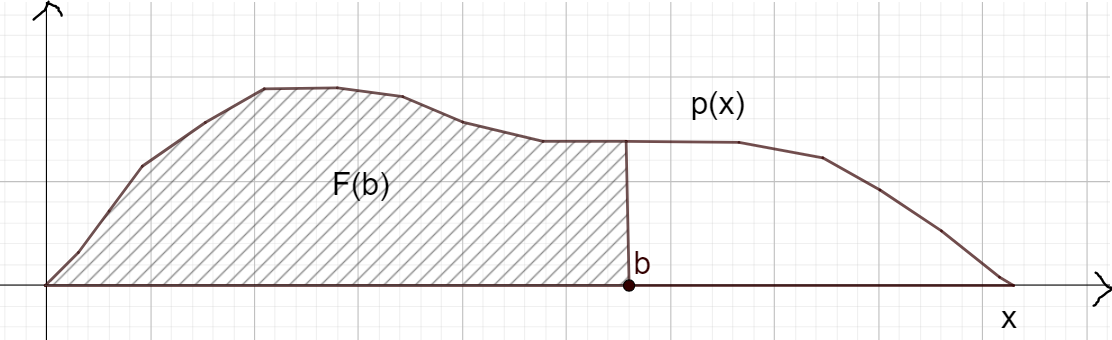
Jos lasketaan todennäköisyyttä sille, että muuttujan arvo on joidenkin arvojen välissä, periaate on alla olevan kuvan mukaan seuraava: Lasketaan ensin todennäköisyys \(P(x\leq b)\). Sen jälkeen vähennetään siitä todennäköisyys \(P(x\leq a\)). Jäljelle jäävä todennäköisyys vastaa kuvassa käyrän ja vaaka-akselin väliin jäävää harmaalla merkittyä aluetta.