Normaalijakauman luottamusvälit

Virhemarginaaleja voidaan usein, mutta ei aina, laskea normaalijakauman avulla. Lasku voidaan tehdä, jos otoskoko on riittävän suuri (vähintään 30) tai jos tiedetään, mikä on populaation mitattavan ominaisuuden todellinen keskihajonta.

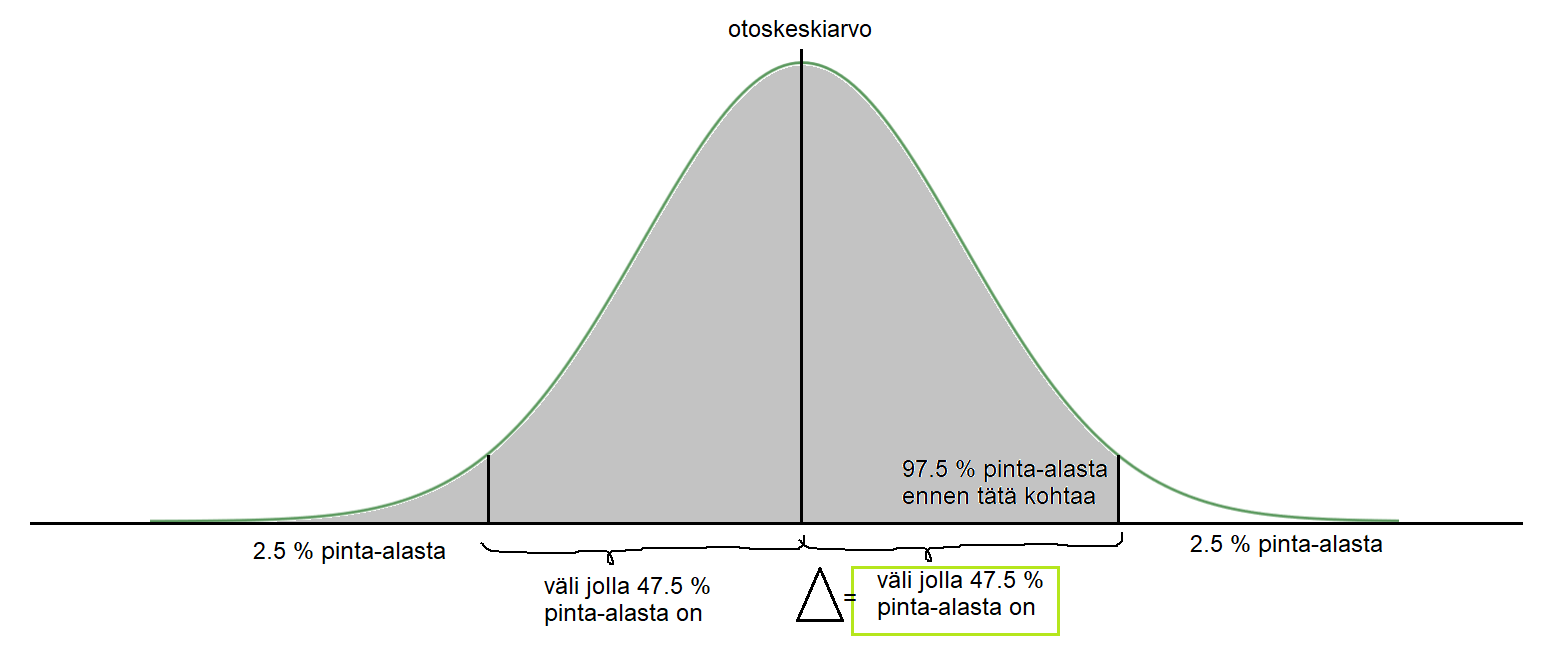
Oletetaan, että otoskeskiarvo noudattaa normaalijakaumaa \(N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)\). Tällaisesta jakaumasta esimerkiksi 95 % luottamustason mukaisen välin saa etsimällä keskiarvon molemmin puolin symmetrisesti rajat, joiden välillä on 95 % jakauman käyrän ja vaaka-akselin pinta-alasta. Tällöin siis alarajan vasemmalle puolelle ja ylärajan oikealle puolelle jää yhteensä 5 % pinta-alasta.

Koska jakauma on symmetrinen, niin kumpaakin päähän jäävä alue on puolet tästä eli 2.5 %. Niinpä virhemarginaali \(\Delta\) on normaalijakauman \(N\left(\mu,\frac{σ}{\sqrt{n}}\right)\) pinta-alaa 0.975 vastaavan muuttujan \(X\) arvon ja otoskeskiarvon erotus.

Esim. Pölynimurien valmistaja tutki 80 imurin erästä, milloin normaalikäytössä tulee tarve ensimmäiselle huollolle. Otoksen keskiarvo oli 720 h ja keskihajonta 209 h. Määritä 99 % luottamusväli ajankohdalle, jolloin ensimmäisen huollon tarve ilmenee.

Ratkaisu

Tiheysfunktion ja vaaka-akselin väliin jäävän pinta-alan on oltava 99 % koko pinta-alasta, joten kumpaankin päähän jää \(\frac{1~\%}{2} = 0.5~\%\). Muuttujan arvon alaraja on siis 0.5 % kohdalla ja yläraja 99.5 % kohdalla.

Excelillä yläraja saadaan komennennolla NORMAALI.JAKAUMA.KÄÄNT(99,5%;720;23,4), vastaus 780, ja alaraja saadaan NORMAALI.JAKAUMA.KÄÄNT(0,5%;720;23,4), vastaus 660.

Huollon tarve ilmenee siis 99 % todennäköisyydellä 660 ja 780 käyttötunnin välillä.

Virhemarginaalin laskemiseen on olemassa Excelissä valmis funktio LUOTTAMUSVÄLI.NORM, johon parametriksi tulee valittu merkitsevyystaso, otoksen keskihajonta ja otoskoko. Edellisen esimerkiksi tapauksessa virhemarginaali laskettaisiin LUOTTAMUSVÄLI.NORM(0,01;209;80), josta tulokseksi tulee noin 60. Luottamusvälin alaraja olisi siis 720 h - 60 h=660 h ja yläraja 720 h + 60 h=780 h.

Esim. Populaatiosta, jonka tiedetään olevan normaalisti jakautunut keskihajontana 0.3, otetaan seuraava otos: {12.6, 13.4, 12.8, 13.2}. Muodosta keskiarvon 95 % luottamusväli.

Ratkaisu

Otoskoko on \(n=4\), keskihajonta \(\sigma=0.3\), ja merkitsevyystaso on \(\alpha=1-0.95=0.05\).

Lasketaan lisäksi otoskeskiarvo \(\bar{X}=13.0\) ja keskiarvon keskivirhe \(\frac{0.3}{\sqrt{4}}=0.15\).

Nyt todellinen keskihajonta on tiedossa, joten normaalijakaumaa voidaan käyttää, vaikka otoskoko onkin pieni.

Excel: LUOTTAMUSVÄLI.NORM(0,05;0,3;4), tulos 0.294 eli noin 0.3.

Luottamusvälin yläraja on siis noin \(13+0.3=13.3\) ja alaraja \(13-0.3=12.7\).

Toinen tapa on laskea normaalijakauman käänteisfunktion avulla ylä- ja alaraja.

Excel:

NORMAALI.JAKAUMA.KÄÄNT(97,5%;13;0,3/NELIÖJUURI(4)), tulos 13.294 NORMAALI.JAKAUMA.KÄÄNT(2,5%;13;0,3/NELIÖJUURI(4)), tulos 12.706