Logaritmimalli

Logaritmimalli \(y=a+b \ln{⁡x}\) sopii tilanteeseen, jossa kasvu tai väheneminen on ensin nopeaa ja tasaantuu sitten. Merkintä \(\ln\) tarkoittaa luonnollista eli \(e\)-kantaista logaritmia. Luku \(e\) on nimeltään Neperin luku ja sen likiarvo on noin 2.72. Esimerkiksi \(\ln{20} \approx 2.996\), sillä \(e^{2.996}\) on noin 20.

Mallissa luvun \(x\) pitää olla suurempi kuin nolla. Jos \(b < 0\), kyse on vähenemisestä, ja jos \(b > 0\), kyse on kasvamisesta. Myös logaritmimallin voi sovittaa dataan Excelin trendiviiva-toiminnon avulla.

Logaritmimalliin kannattaa muuttujan \(x\) arvoiksi valita melko pieniä lukuja, jotta mallin sovitus on luotettava. Esimerkiksi jos muuttujana on aika vuosien 1950-2020 välillä, kannattaa konkreettisen vuosiluvun sijasta käyttää muuttujan arvona esimerkiksi aikaa vuodesta 1949 laskettuna.

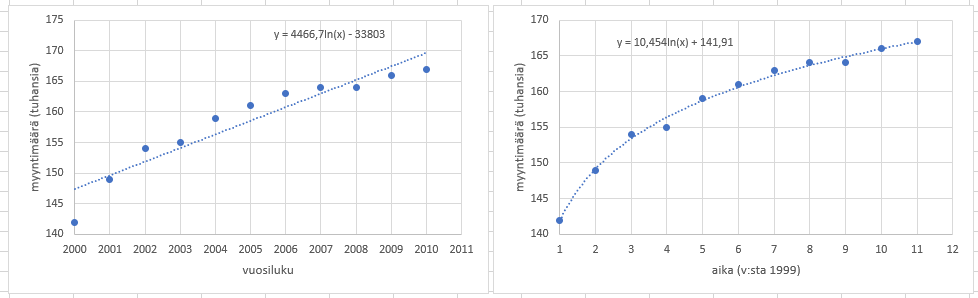
Alla olevat kuvat esittävät kuvitteellisen tietokonepelin myyntimääriä ajan funktiona. Kuvaajissa on käytetty muuten samaa dataa, mutta vasemmalla muuttujana on käytetty vuosilukua, oikealla taas kulunutta aikaa tietystä vuodesta laskettuna. Vasemmanpuoleinen malli näyttäisi antavan tulevaisuuden myyntimäärille hieman liian rohkeita ennusteita.