Fractions#
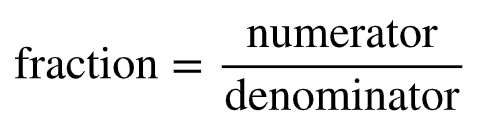
Fig. 9 The top number is called a numerator and the bottom number is called s denominator.#
Multiplication of fractions#
We start with the multiplication of fractions, because it is the simplest and the easiest to evaluate (and since we need it later in finding a common denominator).
To calculate the product of fractions, just multiply the numerators and denominators separately.
\(\frac{a}{c}\cdot\frac{b}{d}=\frac{a\cdot b}{c\cdot d}=\frac{ab}{cd}\), where \(a{,}b{,}c{,}d\ \in\mathbb{Z}\)
Example
\(\frac{5}{8}\cdot\frac{3}{10}=\frac{5\cdot3}{8\cdot10}=\frac{15}{80}\) but the product is not yet simplified. Always remember to simplify!
We can simplify the final product as \(\frac{15}{80}=\frac{3\cdot5}{16\cdot5}=\frac{3}{16}\)
but usually it makes things a bit easier to simplify already before that.
\(\frac{5}{8}\cdot\frac{3}{10}=\frac{5\cdot3}{8\cdot10}=\frac{1\cdot3}{8\cdot2}=\frac{3}{16}\)
Division of fractions#
To calculate the quotient of fractions, change the division into multiplication by using the reciprocal (or inverse) of the divisor.
\(\frac{a}{c}:\frac{b}{d}=\frac{a}{c}\cdot\frac{d}{b}=\frac{a\cdot d}{c\cdot b}=\frac{ad}{cb}\) , where \(a{,}b{,}c{,}d\ \in\mathbb{Z}\)
Example
\(\frac{3}{8}:\frac{9}{4}=\frac{3}{8}\cdot\frac{4}{9}=\frac{3\cdot4}{8\cdot9}=\frac{1\cdot1}{2\cdot3}=\frac{1}{6}\)
Addition of fractions#
Like fractions#
if the denominators are the same, only add the numerators together.
\(\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\), where \(a{,}b{,}c\ \in\mathbb{Z}\)
Example
\(\frac{1}{7}+\frac{4}{7}=\frac{1+4}{7}=\frac{5}{7}\)
Unlike fractions#
if the denominators are not the same, find the common denominator. This can be achieved by using a equation of
\(\frac{a}{c}+\frac{b}{d}=\frac{ad+cb}{cd}\), where \(a{,}b{,}c{,}d\ \in\mathbb{Z}\)
but usually it is not the simplest way.
Example
\(\frac{2}{3}+\frac{1}{9}\)
Method 1. Using the equation
\(\frac{2}{3}+\frac{1}{9}=\frac{2\cdot9+3\cdot1}{3\cdot9}=\frac{18+3}{27}=\frac{21}{27}=\frac{3\cdot7}{3\cdot9}=\frac{7}{9}\)
Method 2. Using your own skills
Here the least common multiple of 3 and 9 is 9, because \(3\cdot3=9\) and \(1\cdot9=9\). So we multiply the first fraction by a whole fraction \(\frac{3}{3}\).
\(\frac{2}{3}+\frac{1}{9}=\frac{3}{3}\cdot\frac{2}{3}+\frac{1}{9} =\frac{3\cdot2}{3\cdot3}+\frac{1}{9} =\frac{6}{9}+\frac{1}{9} =\frac{7}{9}\)
A common multiple of the denominators can always be found by multiplying the denominators together. You can always use this trick to find a common multiple of the denominators, but then you usually have to simplify the fraction later.
A common multiple of 3 and 9 can be found by multiplying them together: \(3\cdot9=27\). So we multiply the first fraction by a whole fraction of \(\frac{9}{9}\) and the second by a whole fraction of \(\frac{3}{3}\).
\(\frac{2}{3}+\frac{1}{9}=\frac{9}{9}\cdot\frac{2}{3}+\frac{3}{3}\cdot\frac{1}{9}\)
\(=\frac{9\cdot2}{9\cdot3}+\frac{3\cdot1}{3\cdot9}\)
\(=\frac{18}{27}+\frac{3}{27}\)
\(=\frac{18+3}{27}\)
\(=\frac{21}{27}\)
\(=\frac{7}{9}\)
Subtraction of fractions#
Like fractions#
just like in the case of addition, if the denominators are the same, only subtract the numerators.
\(\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}\), where \(a{,}b{,}c\ \in\mathbb{Z}\)
Example
\(\frac{3}{4}-\frac{5}{4}=\frac{3-5}{4}=\frac{-2}{4}=-\frac{1}{2}\) Always remember to simplify your answer!
Unlike fractions#
if the denominators are not the same, again find the common denominator.
\(\frac{a}{c}-\frac{b}{d}=\frac{ad-cb}{cd}\), where \(a{,}b{,}c{,}d\ \in\mathbb{Z}\)
Example
\(\frac{2}{5}-\frac{1}{3}\)
Method 1. Using the equation
\(\frac{2}{5}-\frac{1}{3}=\frac{2\cdot3-5\cdot1}{5\cdot3}=\frac{6-5}{15}=\frac{1}{15}\)
Method 2. Using your own skills
Here the least common multiple of 5 and 3 is 15, because \(3\cdot5=15\) and \(5\cdot3=15\). So we multiply the first fraction by a whole fraction of \(\frac{3}{3}\) and the second by a whole fraction of \(\frac{5}{5}\).
\(\frac{2}{5}-\frac{1}{3}=\frac{3}{3}\cdot\frac{2}{5}-\frac{5}{5}\cdot\frac{1}{3}\)
\(=\frac{3\cdot2}{3\cdot5}-\frac{5\cdot1}{5\cdot3}\)
\(=\frac{6}{15}-\frac{5}{15}\)
\(=\frac{6-5}{15}\)
\(=\frac{1}{15}\)
