Basic vector calculus

Addition, substraction and scalar multiplication

The sum of vectors \(\overline{u}\) and \(\overline{v}\) is denoted by \(\overline{u}+\overline{v}\). The sum is a new vector, sometimes called a resultant vector. The tail of the resultant vector is the tail of vector \(\overline{u}\) and its head can be found from the head of vector \(\overline{v}\) after it is placed at the head of vector \(\overline{u}\), as in figure below.

The difference of vectors \(\overline{u}\) and \(\overline{v}\) is denoted by \(\overline{u}-\overline{v}\). Here the opposite of vector \(\overline{v}\) is added to the head of vector \(\overline{u}\) as \(\overline{u}+(-\overline{v})\).

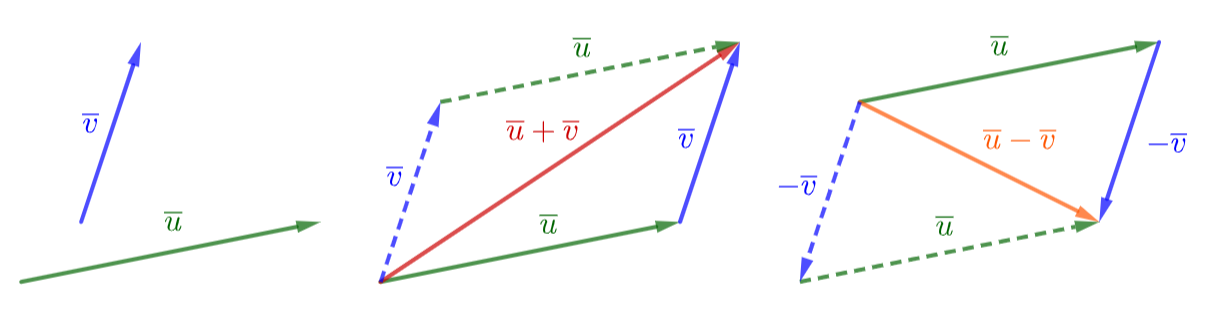
Fig. 11 Addition and substraction of vectors in a plane

For all vectors and scalars we can write the following axioms in real vector space:

Addition
Commutativity	\(\overline{u}+\overline{v}=\overline{v}+\overline{u}\)
Commutativity	\(\overline{u}-\overline{v}=-\overline{v}+\overline{u}\)
Associativity	\(\overline{u}+(\overline{v}+\overline{w})=(\overline{u}+\overline{v})+\overline{w}\)
Identity element	\(\overline{u}+\overline{0}=\overline{u}\)
Inverse element	\(\overline{u}+(-\overline{u})=\overline{0}\)

Scalar multiplication	NB: the dot \(\cdot\) is not be used in scalar multiplication!
Commutativity	\(\overline{u}r=r\overline{u}\)
Associativity	\(s(r\overline{u})=(sr)\overline{u}\)
Distributivity	\(r(\overline{u}+\overline{v})=r\overline{u}+r\overline{v}\)
Distributivity	\((r+s)\overline{u}=r\overline{u}+s\overline{u}\)

EXAMPLE 1. Addition, substraction and scalar multiplication

Let’s examine vectors \(\overline{u}=(5, 2)\) and \(\overline{v}=(1, 3)\). When vectors are added or substracted (the sum or substraction is calculated), corresponding components are calculated separately. When a vector is multiplied by a scalar, every component of the vector is multiplied.

\(\text{a)}\) Addition

\(\begin{align}\overline{u}+\overline{v}&=(5, 2)+(1, 3) \\ \\ &=(5+1, 2+3) \\ \\ &=(6, 5)\end{align}\)

---

\(\text{b)}\) Substraction

\(\begin{align}\overline{u}-\overline{v}&=(5, 2)-(1, 3) \\ \\ &=(5-1, 2-3) \\ \\ &=(4,-1)\end{align}\)

---

\(\text{c)}\) Scalar multiplication

\(\begin{align}2\overline{u}&=2(5, 2) \\ \\ &=(2\cdot5, 2\cdot2) \\ \\ &=(10, 4)\end{align}\)

---

\(\text{d)}\) Linear combination (“a mix of all the above”)

\(\begin{align}-2\overline{u}+3\overline{v}&=-2(5, 2)+3(1, 3) \\ \\ &=(-2\cdot5, -2\cdot2)+(3\cdot1, 3\cdot3) \\ \\ &=(-10, -4)+(3, 9) \\ \\ &=(-10+3,-4+9) \\ \\ &=(-7,5)\end{align}\)

Definition

Any vector in a plane can be presented as a linear combination of two non-parallel vectors.

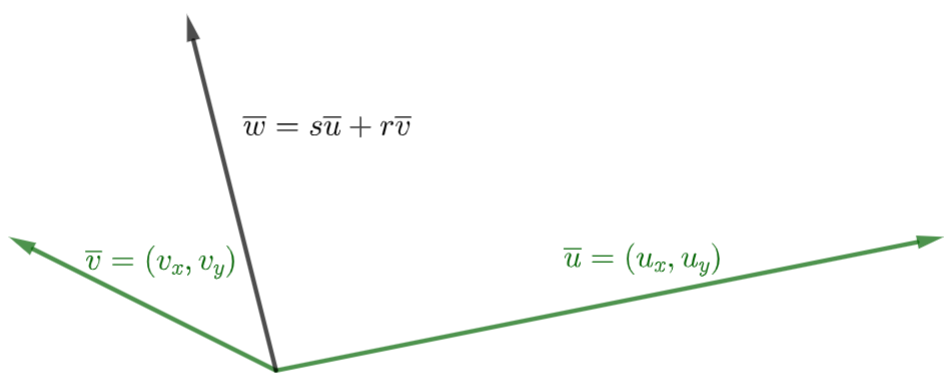
Fig. 12 Vector \(\overline{w}\) as a linear combination of vectors \(\overline{u}\) and \(\overline{v}\)

EXAMPLE 2. Finding the linear combination

Can vector \(\overline{c}=(4, -3)\) be presented as a linear combination of vectors \(\overline{a}=(5, 6)\) and \(\overline{b}=(-2, -5)\)?

Vectors \(\overline{a}\) and \(\overline{b}\) are clearly non-parallel, so linear combination is possible. This can be verified by dot product of vectors, which will be discussed later in material (Link missing to dot product).

Now all we have to do is to find scalars r ja s so that \(r\overline{a}+s\overline{b}=\overline{c}\). Let’s form an equation from this.

\[\begin{split}\begin{align}r\overline{a}+s\overline{b}&=\overline{c} \\ \\ r(5, 6) +s(-2, -5)&=(4, -3) \\ \\ (5r, 6r)+(-2s, -5s)&=(4, -3) \\ \\ (5r-2s, 6r-5s)&=(4, -3)\end{align}\end{split}\]

If the equation above is true, we can consider the x- and y-components separately. Thus we have a system of two equations:

\[\begin{split}\begin{cases} 5r-2s=4 \\ 6r-5s=-3 \end{cases}\end{split}\]

A solution can be found that \(r = 2\) and \(s = 3\). (Link missing to systems of equations.) Because we have shown that scalars s and r exist, $\(\overline{c}=2\overline{a}+3\overline{b}\)$.

Vector norm

Magnitude of a vector, the vector norm, is by definition always a non-negative scalar and is denoted as the absolute of a vector. In a plane the norm is calculated with the help of Pythagorean theorem, since a vector is described by two perpendicular components. However, the norm of a vector can be calculated for any dimensional vector \(\overline{v}\) as

\[\left|\overline{v}\right|=\sqrt{\sum_{k=1}^nv_k^2}=\sqrt{v_x^2+v_y^2+v_z^2+...}\]

Fig. 13 Pythagorean theorem for right triangle, when the length of the legs are 4 and 3

Python code

# define vector
v = np.array([4, 3]) 

# calculate vector norm
np.sqrt(np.sum(v**2))  

As in figure above, the norm of the vector \(\overline{u}=(4, 3)\) can be calculated as

\(\begin{align}|\overline{u}|&=\sqrt{4^2+3^2} \\ \\ &=\sqrt{16+9} \\ \\ &=\sqrt{25} \\ \\ &=5\end{align}\)

EXAMPLE 3. Norm is known but components are not

a) Solve such a positive scalar y that the norm of vector \(\overline{u}=\left(-1,y\right)\) is 5.

b) Solve such a positive scalar s that the norm of vector \(\overline{v}=(s, 3s)\) is 10.

Solution

a) We need to solve the value of the y-component, when the x-component is -1 and the magnitude of the vector is 5. Let’s form an equation for the norm and solve y.

\(\begin{align}|\overline{u}|&=5 \\ \\ \sqrt{(-1)^2+y^2}&=5 \\ \\ \sqrt{1+y^2}&=5\ ||\left(\ \ \right)^2 \\ \\ 1+y^2&=25 \\ \\ y^2&=25-1 \\ \\ y^2&=24\ ||\sqrt{\ \ } \\ \\ y&=\pm\sqrt{24} & \text{only positive value is considered} \\ \\ y&=\sqrt{4\cdot6} \\ \\ y&=2\sqrt6\end{align}\)

b) We need to solve a value for the coefficient s so that the y-component is three times bigger than the x-component. When the norm of the vector is 10, let’s form a equation for the norm.

\(\begin{align}|\overline{v}|&=10 \\ \\ \sqrt{s^2+(3s)^2}&=10 \\ \\ \sqrt{s^2+9s^2}&=10 \\ \\ \sqrt{{10s}^2}&=10\ ||\left(\ \ \right)^2 \\ \\ 10s^2&=100\ ||:10 \\ \\ s^2&=10\ ||\sqrt{\ \ } \\ \\ s&=\pm\sqrt{10} & \text{only positive value is considered} \\ \\ s&=\sqrt{10}\end{align}\)