Position vector and displacement vector#
As noted, vectors are defined solely by their magnitude and direction. Therefore, the beginning point (the tail) of a vector can be anywhere and it’ still the same vector. When the tail is located in the Origin, the vector is called a position vector.
Definition
A coordinate point \(A=(x, y)\) in a plane corresponds to a position vector \(\overline{OA}=(x, y)\), which has its tail in the Origin and the head in coordinate point A. In 3D space, the (x, y, z)-coordinate system, a coordinate point \(B=(x, y, z)\) corresponds to a position vector \(\overline{OB}=(x, y, z)\).
The magnitude of the position vector \(|\overline{OA}|\) corresponds to the distance from Origin to point A.
EXAMPLE 1. Position vectors
Let’s create position vectors corresponding to coordinate points \(A=(-2, 0)\), \(B=(1, 3)\) and \(C=(3, -1)\) and calculate the sum of them \(\overline{OP}=\overline{OA}+\overline{OB}+\overline{OC}\). Where is the head of the vector \(\overline{OP}\) located and how long is it (what is its magnitude)?
Position vectors from Origin to coordinate points \(A, B\) and \(C\) are
\(\begin{align}\overline{OA}&=(-2, 0) \\ \overline{OB}&=(1, 3) \\ \overline{OC}&=(3, -1)\end{align}\)
The resultant vector is
\(\begin{align}\overline{OP}&=\overline{OA}+\overline{OB}+\overline{OC} \\ \\ &=(-2, 0)+(1, 3)+(3, -1) \\ \\ &=(2, 2)\end{align}\)
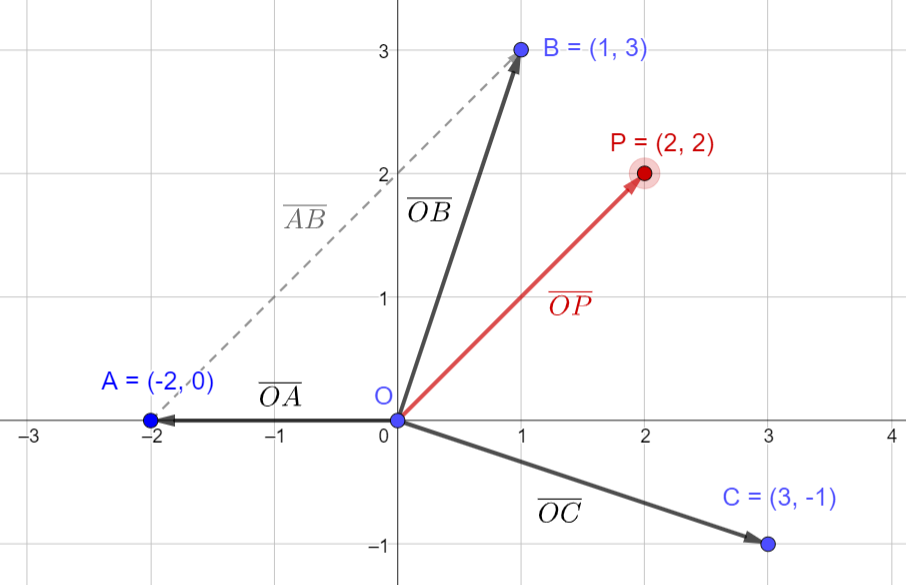
Fig. 16 Addition of position vectors and the resultant vector \(\overline{OP}\)#
Since the tail of position vector \(\overline{OP}\) is in Origin, the coordinates of its head are \(P=(2, 2)\).
Magnitude is calculated as \(|\overline{OP}|=\sqrt{2^2+2^2}=\sqrt8=\sqrt{4\cdot2}=2\sqrt2\)
Displacement vector expressed by position vectors#
Let’s examine the vector \(\overline{AB}\) in the previous example (Click to show) Vector from point \(A\) to point \(B\) can be written as the sum of vectors \(\overline{AO}\) and \(\overline{OB}\).
Definition
A displacement vector \(\overline{AB}\) is the shortest distance between coordinate points A and B and is formulated by substracting the position vector of its tail from the position vector of its head.
As in the figure in EXAMPLE 1., the displacement vector \(\overline{AB}\) can be formed as
\(\begin{align}\overline{AB}&=\overline{OB}-\overline{OA} \\ \\ &=(1, 3)-(-2, 0)=(3, 3)\end{align}\)
EXAMPLE 2. Orienteering
Orienteerer starts from control point \(A=(150, 200)\) and runs to point \(C\) through point \(B=(340, 320)\). Calculate the shortest distance from control point \(A\) to point \(C\), when displacement vector \(\overline{BC}=(60, 300)\).
Solution
Let’s determine the displacement vector \(\overline{AC}\) as the sum of displacement vectors \(\overline{AB}\) and \(\overline{BC}\).
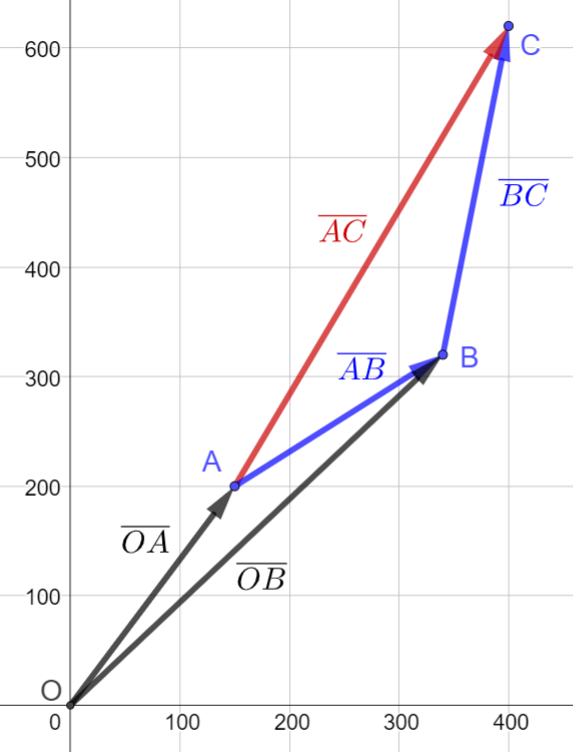
Fig. 17 The route of the orienteerer from control point A to point B.#
First we need to formulate the displacement vector \(\overline{AB}\). This can be done as the substraction of position vectors \(\overline{OA}\) and \(\overline{OB}\).
\(\begin{align}\overline{AB}&=\overline{OB}-\overline{OA} \\ \\ &=(340, 320)-(150, 200) \\ \\ &=(340-150, 320-200) \\ \\ &=(190, 120)\end{align}\)
As in figure 7., we can now determine the displacement vector \(\overline{AC}\).
\(\begin{align}\overline{AC}&=\overline{AB}+\overline{BC} \\ \\ &=(190, 120)+(60, 300) \\ \\ &=(190+60, 120+300) \\ \\ &=(250, 420)\end{align}\)
Finally, let’s calculate the magnitude of displacement vector \(\overline{AC}\).
\(\begin{align}|\overline{AC}|&=\sqrt{250^2+420^2} \\ \\ &=\sqrt{238900} \\ \\ &=488.773\ldots \\ \\ &\approx490\end{align}\)
Answer: the shortest distance from control point \(A\) to point \(C\) is approximately 490 metres.
