Preface#
Vector, as a mathematical object, is only about 200 years old term. Initially one may come across with vectors as quantities in geometry, space and physics. Therefore computer models about real world and game engines rely on vectors. Vectors are also used in many branches of technology such as GPS localisation, image and graphics prosessing, robotics and of course, machine learning.
Basic concepts#
Scalars are described solely by their magnitude but vectors also have direction. For instance speed, acceleration and force are vectors. In cartesian coordinate system, also know as the (x, y)-coordinate system or plane, vectors can describe the number of steps taken horizontally and vertically. The direction can also be to negative.
However, the location of a vector is not defined by in its definition. A vector can ne used describe the shortest route between two coordinate points. When a vector is defined this way, we use the term displacement vector.
Instructions
You can move the beginning point A, the tail, and the ending point B, the head, of the displacement vector \(\overline{AB}\) with your mouse and see how the components of the vector change.
Vectors are comprised by two components in the cartesian plane just as coordinate points are. Where coordinate points describe the exact location of a single point, the components of a vector describe its length correspondingly. In the applet above the displacement vector from point A to point B is comprised of the component parallel to the x-axis (green dashed arrow) and of the component parallel to the y-axis (red dashed arrow). The components of the displacement vector are expressed in brackets as \(\overline{AB}=(x, y)\). Vectors can also be described in the polar coordinate system or as a single column or row matrix, and these will be handled later in the material.
Definition, angles
Direction angle of a vector \(\theta\) is measured to the counterclockwise direction from the positive x-axis.
Angle between two vectors (between 0° … 180°) is defined so that the tail of the two vectors is in the same coordinate point and the angle is measured counterclockwise.
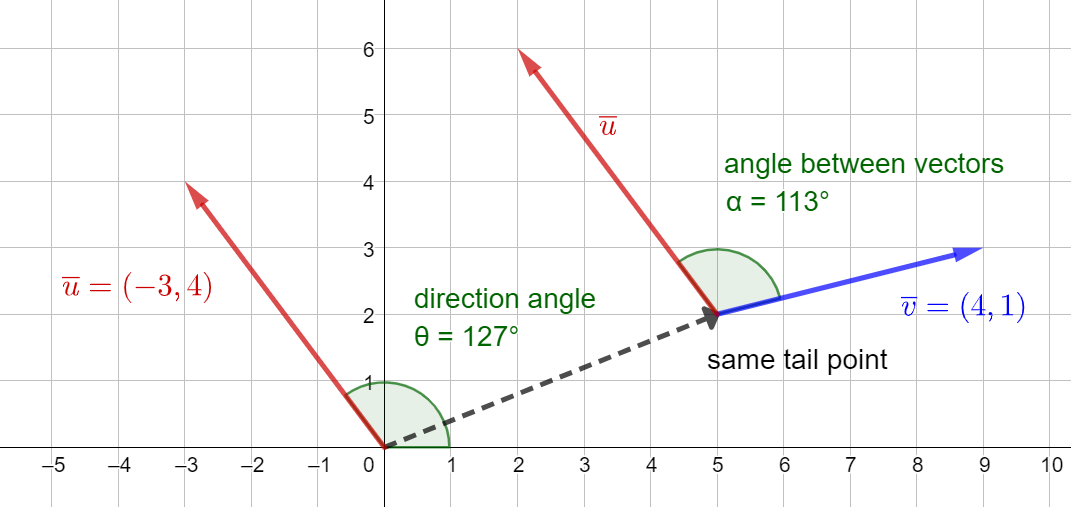
Fig. 11 Examples of the direction angle and the angle between vectors#
Notations#
Vectors are usually denoted with a lower case letter with an overline (or a bar), for instance \(\overline{u}\), \(\overline{v}\), \(\overline{w}\). In the case of a displacement vector, vectors are usually denoted by their tail and head coordinate points as \(\overline{AB}\). An arrow above the letter \(\vec{u}\) or letters \(\overrightarrow{AB}\) is also used. In order to denote vectors in a fast way, letters can be written simply in bold, for instance u or AB. In this study material vectors are denoted with an overline and coordinate points are denoted by capital letters, for instance the origin is denoted as \(O = (0, 0)\).
Length of a vector is denoted as absolute value \(|\overline{u}|\) or \(|\overline{AB}|\)
When vectors are nonparallel, \(\overline{u}\nparallel\overline{v}\) is used
When vectors are perpendicular, \(\overline{u}\perp\overline{v}\) is used
When vectors are parallel, \(\overline{u}\parallel\overline{v}\) is used (note: this can mean that the vectors are in the same direction or the opposite direction)
Vectors are in the same direction \(\overline{u}\uparrow\uparrow\overline{v}\)
Vectors are in the opposite direction \(\overline{u}\uparrow\downarrow\overline{v}\)
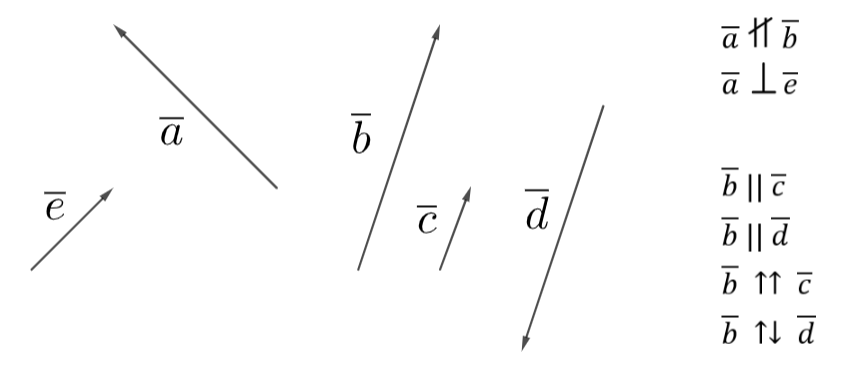
Fig. 12 Examples of vectors in a plane#
