Ctrl+K

Sets of numbers

Sets of numbers#

The set of natural numbers is denoted by the symbol \(\mathbb{N}\). It includes the whole numbers starting from zero \(\{0{,}1{,}2{,}3{,}...\}\), sometimes called as the “naturals”.

Natural numbers without zero \(\mathbb{N}^+=\left\{1{,}2{,}3{,}...\right\}\) are also called as “counting numbers”.

The set of integers is denoted by \(\mathbb{Z}=\{...{,}-3{,}-2{,}-1{,}0{,}1{,}2{,}3{,}...\}\)

Positive integers are denoted as \(\mathbb{Z}^+=\{1{,}2{,}3{,}...\}\), which is actually the same set as \(\mathbb{N}^+\). As a subset, this can be denoted by \(\mathbb{N}^+\subseteq\mathbb{Z}^+\) and \(\mathbb{Z}^+\subseteq\mathbb{N}^+\), since every element of \(\mathbb{N}^+\) is also an element of \(\mathbb{Z}^+\).

Negative integers \(\mathbb{Z}^-=\{...{,}-3{,}-2{,}-1\}=\mathbb{Z}-\mathbb{N}\). Here the notation \(\mathbb{Z}-\mathbb{N}\) (or \(\mathbb{Z}\ \setminus\mathbb{N}\)) means that the elements of natural numbers are removed from the set of integers. See set difference.

EXAMPLE 1. the number \(4k-5{,}\ k\in\mathbb{Z}\) is always odd

Proof:

\(\begin{align} 4k-5 & =(4k-6)+1 \\ \\ & =2(2k-3)+1{,}\ k\in\mathbb{Z} \end{align}\)

What we have shown is that the \(2(2k-3)\) is always even for every value of \(k\), because the coefficient in front of the brackets is \(2\). Therefore \(2(2k-3)+1=4k-5\) is always odd.

Rational numbers \(\mathbb{Q}\), or the “fractions”, are denoted by

\(\mathbb{Q}=\{\frac{m}{n}\mid\ m{,}n\ \in\mathbb{Z}{,}\ n\ne0\}\)

Includes numbers whose decimal expasion terminates, e.g \(\frac{3}{5}=0.6\) or decimal expansion begins to repeat a finite sequence e.g. \(\frac{13}{17}=0.76470588235294117647058823529411...\), where the repeating finite sequence is \(7647058823529411\).

When numbers cannot be expressed as a ratio of two integers, they are called irrational numbers. For instance \(\sqrt{2}=1.414...\) and \(pi{,}\ \pi=3.14159...\) are irrational numbers. Here decimal expansion does not terminate nor end with a repeating finite sequence.

Real numbers \(\mathbb{R}\) include rational and irrational numbers. We can call this as a union of rational and irrational numbers. Therefore, irrational numbers can be expressed as \(\mathbb{R}\) \ \(\mathbb{Q}\).

Real numbers correspond to all the points on a number line.

Complex numbers \(\mathbb{C}\) can be expressed as a sum of a real part \(a\) and an imaginary part \(bi\) as \(a+bi\), where \(a{,}b\in\mathbb{R}\) and \(i\) is the imaginary unit, which is denoted as \(i^2=-1\Leftrightarrow i=\sqrt{-1}\).

The imaginary part \(bi{,}\ b\in\mathbb{R}\) actually forms the set of imaginary numbers \(\mathbb{I}\), in which real numbers are multiplied by the imaginary unit. Complex numbers correspond to all the points on a comlex plane, where the horizontal axis represents the real part and the vertical axis represents the imaginary part.

Every set of numbers is a “proper” subset of larger one, excluding the set of complex numbers: \(\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}\). This can be presented as an Euler diagram:

Sets of numbers presented in an Euler diagram

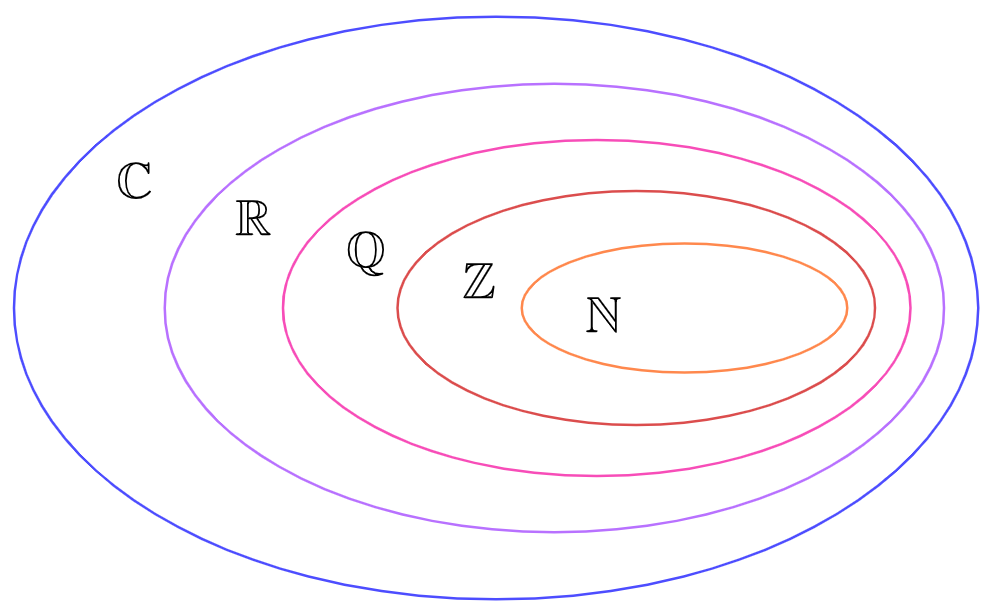
Fig. 7 Sets of numbers presented in an Euler diagram#

  • Natural numbers are a proper subset of integers.

  • Integers are a proper subset of rational numbers.

  • Rational numbers are a subset of the real numbers.

  • Union of rational and imaginary numbers makes up the real numbers.

  • Complex Numbers are the superset of all other sets.

Axioms for the real numbers#

For all real numbers \(a\), \(b\) and \(c\) \(\left(a{,}b{,}c\in\mathbb{R}\right)\), following axioms are satisfied.

Addition

  • Commutative: \(a+b=b+a\)

  • Associative: \(a+(b+c)=(a+b)+c\)

  • Number Zero: a real number \(0\) exists so that \(a+0=a\)

  • Inverse: a real number \(-a\) exists so that \(a+\left(-a\right)=0\)

Multiplication

  • Commutative: \(a\cdot b=b\cdot a\)

  • Associative: \(a\cdot(b\cdot c)=(a\cdot b)\cdot c\)

  • Number One: a real number \(1\) exists so that \(a\cdot1=a\).

  • Inverse: if \(a\ne0\) a real number \(\frac{1}{a}=a^{-1}\) exists so that \(aa^{-1}=1\)

  • Distributive: \(a\cdot(b+c)=a\cdot b+a\cdot c\)

Order

  • Either \(a<b\) or \(a>b\) or \(a=b\)

  • If \(a<b\) and \(b<c\), then \(a<c\)

  • \(a<b\) and \(a+c<b+c\) are equivalent

  • If \(a>0\) and \(b>0\), then \(ab>0\)

Contents