Set theory#
Introduction#
Set theory is a branch of mathematics that deals with the study of collections of objects, called sets. These objects can be anything: numbers, letters, colors, or even other sets. Set theory provides a formal framework for understanding and analyzing the relationships between these collections, forming the basis for many areas of mathematics and other disciplines, including
Logic: Sets are used to define truth values and logical operations.
Probability: Set operations are used to define events and calculate probabilities.
Topology: Sets and their properties are used to study the properties of spaces.
Algebra: Groups, rings, and fields are structures built on sets.
Basic concepts#
Sets and Elements: A set is a collection of distinct objects, that share a common characteristic. In set theory, these objects are called elements. A set is denoted by a capital letter, e.g. \(A\), \(B\) and its elements are listed inside curly brackets \(\{\dots\}\). For example, set \(A\) of whole numbers greater than 3 but less than 9 is \(A=\{4, 5, 6, 7, 8\}\). An element either belongs to a set or it doesn’t. When an element belongs to set \(A\), it is denoted as \(4 \in A\). If it doesn’t, the notation is \(3 \notin A\)
Universal set and empty set: The universal set, denoted by \(U\), is the set that contains all the elements under consideration. An empty set is denoted by \(\{\}\) or \(\emptyset\) and contains no elements.
Subset: Set \(A\) is a subset of another set \(B\) if every element of \(A\) is also an element of \(B\). Symbolically this can be expressed as \(A \subseteq B\). If \(A\) is a subset of \(B\) but not equal as \(B\) \((A \not= B)\), it is called a proper subset, and it is denoted by \(A \subset B\).
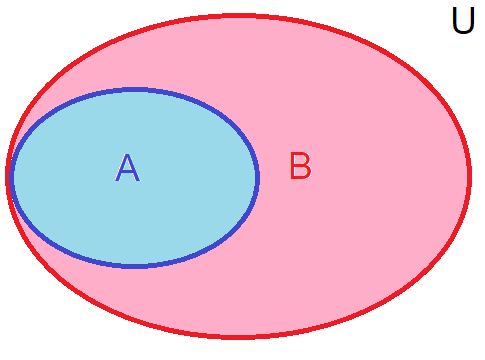
Fig. 1 Set A is a (proper) subset of set B in a Venn diagram.#
\(A \subseteq B\) means that \(A\) is a subset of \(B\), and \(A\) could potentially be equal to \(B\).
\(A \subset B\) means that \(A\) is a proper subset of \(B\), indicating that \(A\) is strictly contained within \(B\) and is not equal to \(B\).
It’s important to note that a set is always considered a subset of itself. That is, if \(A\) is a set, then \(A \subseteq A\).
Complement of a set: The complement of a set \(A\) in relation to the universal set \(U\), denoted by \(\overline{A}\), contains all elements in \(U\) that are not in \(A\). Mathematically, the complement of a \(A\) os defined by \(-A = \{x \in U \mid x \notin A\}\).
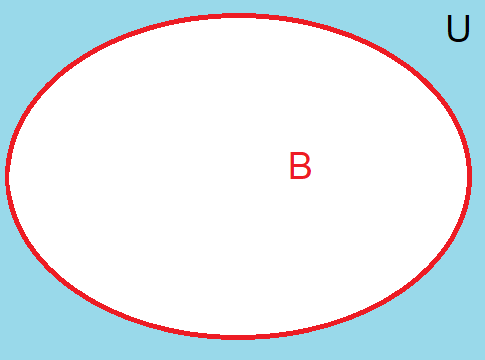
Fig. 2 A complement of set A presented as a Venn diagram.#
Union: The union of \(A\) and \(B\), denoted \(A \cup B\), contains all elements that are in either \(A\) or \(B\), or both. Mathematically put \(A \cup B = \{x \in U \mid x \in A \text{ or } x \in B\}\).
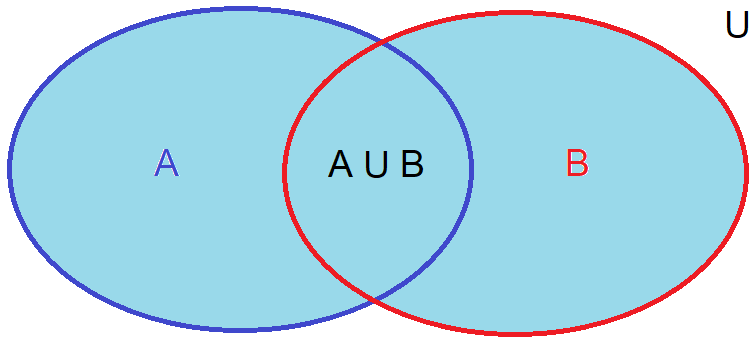
Fig. 3 Union of sets A and B presented in a Venn diagram#
Intersection: The intersection of two sets \(A\) and \(B\), denoted \(A \cap B\), is the set of elements that are in both \(A\) and \(B\). Mathematically \(A \cap B = \{x \in U \mid x \in A \text{ and } x \in B\}\).
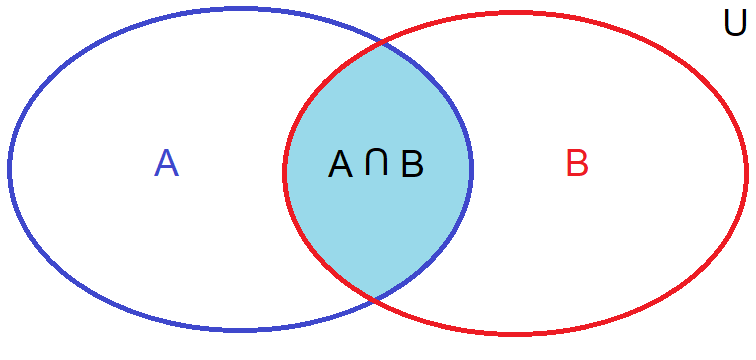
Fig. 4 Intersection of sets A and B presented in a Venn diagram#
Set difference: The set difference between sets \(A\) and \(B\) consists of all the elements that are only in set \(A\) but not in set \(B\). In other words, when you subtract one set from another, \(A-B\) contains the elements that are exclusive to set \(A\) and are not shared with set \(B\). Mathematically \(A-B = \{x \mid x \in A \text{ and } x \notin B\}\).
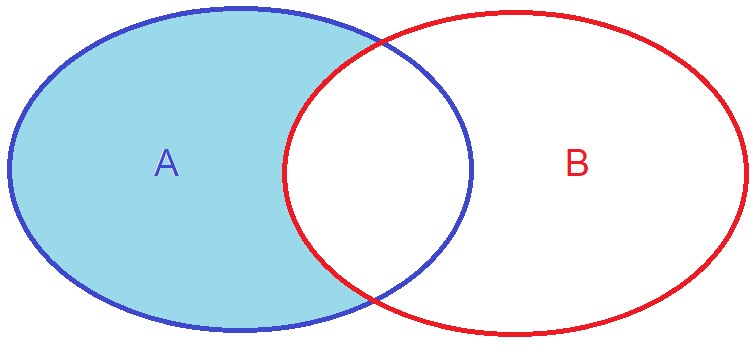
Fig. 5 Intersection of sets A and B presented in a Venn diagram#
Note that usually \(A-B \not= B-A\), so the order of subtraction matters.
In some context, especially in programming and computer sciences, the set difference \(A-B\) can be written as \(A \setminus B\).
Examples#
Let \(A=\{1,2,3\}\), \(B=\{1,2,3,4\}\), \(C=\{3,4,5\}\) and \(U=\{1,2,3, \dots ,9\}\).
a) \(1 \in A\) and \(1 \in B\) but \(1 \notin C\).
b) \(A \subseteq B\) but also \(A \subset B\).
c) Complement of a \(A\) is \(\overline{A}=\{4,5,6,7,8,9\}\).
d) Union of \(A\) and \(C\) is \(A \cup C =\{1,2,3,4,5\}\).
e) Intersection of \(A\) and \(C\) is \(A \cap C =\{3\}\).
f) Set difference of \(A\) and \(C\) is \(A-C=\{1,2\}\) but \(A-B=\emptyset\).
De Morgan’s laws#
De Morgan’s Laws provide a way to manipulate complex statements involving unions, intersections, and complements of sets (or logical statements) by negating the components.
There are two De Morgan’s Laws: one for the negation of a union and one for the negation of an intersection.
First De Morgan’s Law The negation of a union of sets is equivalent to the intersection of the complements of those sets.
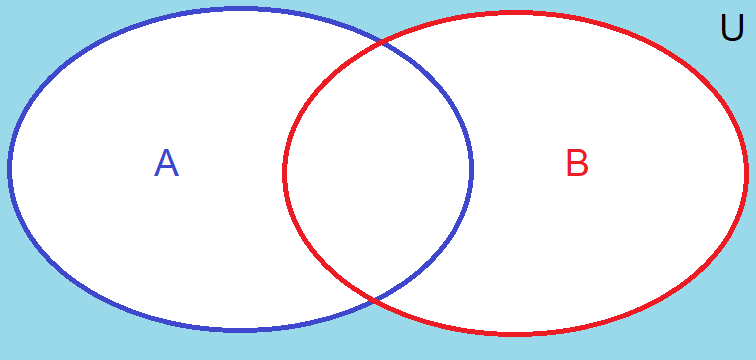
Fig. 6 First De Morgan’s Law presented in a Venn diagram#
Mathematically, this law can be expressed as:
\(\overline{A \cup B} = \overline{A} \cap \overline{B}\).
Second De Morgan’s Law The negation of an intersection of sets is equivalent to the union of the complements of those sets. The negation of a union of sets is equivalent to the intersection of the complements of those sets.
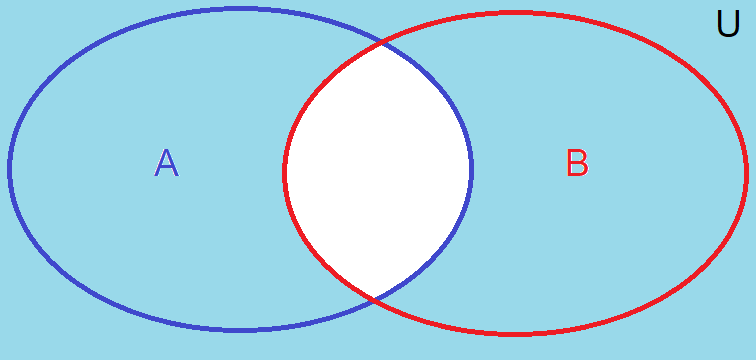
Fig. 7 Second De Morgan’s Law presented in a Venn diagram#
Mathematically, this law can be expressed as: \(\overline{A \cap B} =\overline{A} \cup \overline{B}\)
