Combinatorics#
Combinatorics is a branch of mathematics that deals with counting, arrangement and combination of objects or elements. It focuses on studying the ways in which simple discrete objects can be organized, combined or chosen. For instance, it is pretty easy to compute the amount of numbers with three figures but it is much harder to find all the possible arrengements for a bookshelf.
Multiplication principle#
also known as Rule of product. When making multiple consecutive choices, the total number of possibilities is obtained by multiplying the respective numbers of options available at each choice stage. Intuitively it can expressed as “if there are \(a\) ways of doing something and \(a\) ways of doing another thing, then there are \(a \cdot b\) ways of performing both actions.”
The principle can be described by a tree model.
Example. A student has two knitted caps, two jumpsuits and three pairs of shoes. How many different sets of outfits can be created from these pieces of clothing?
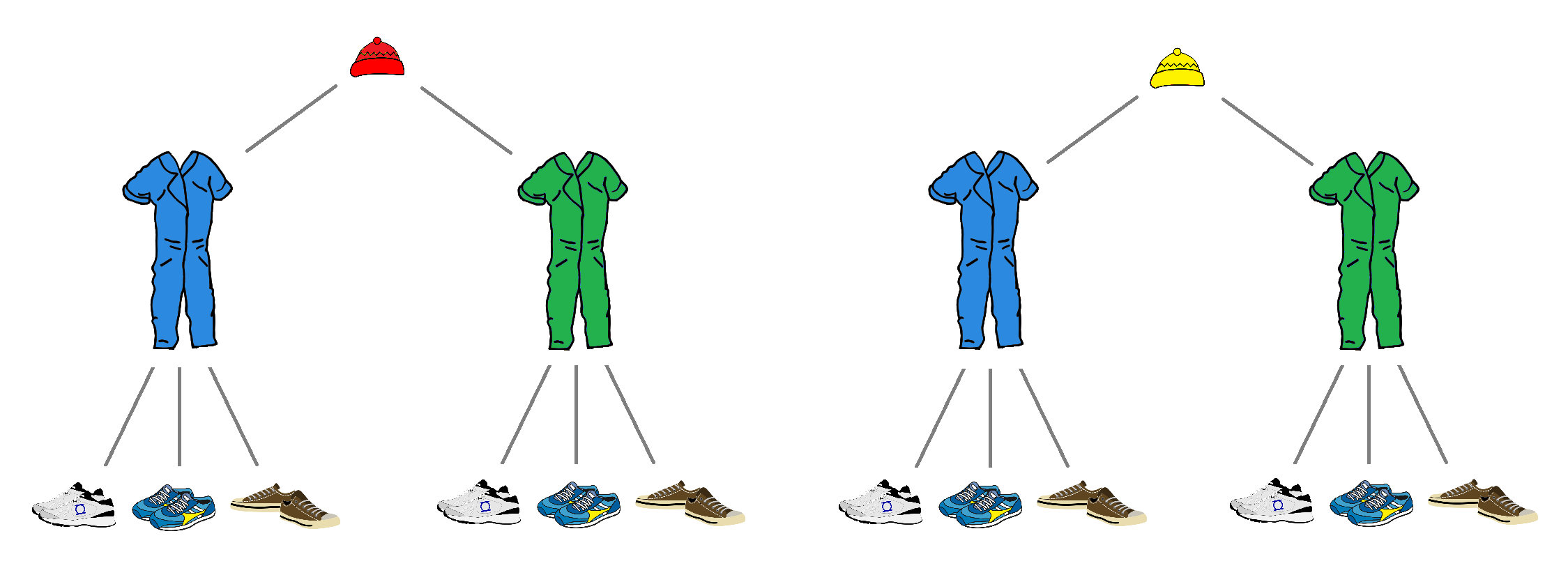
Fig. 18 The number of different sets of outfits can be computed from the bottom row of the tree model.#
The cap can be chosen in two different ways, the jumpsuit can be chosen from two different options and there are three different pairs of shoes. Using the multiplication principle we can compute the number of different sets by \(2 \cdot 2 \cdot 3 = 12\).
EXERCISE 1. 13 Premier League matches
There are 13 Premier League matches happening on the upcoming Saturday and a gambler can choose the result of a match from three different options.
1: home team wins
X: tie
2: away team wins
a) How many different football pools does there exist?
b) What if the number of matches is \(n\)?
Answers: a) 1 594 323
Addition principle#
also known as Rule of sum. The overall number of options of which to choose from can be can be computed by adding the number of separated options. In general, if there are different cases with n1 choices in Case 1, n2 choices in Case 2, and so forth, then the overall number of options is the sum n1 + n2 + … + nk. Intuitively it can expressed as that if we have \(A\) number of ways of doing something and \(B\) number of ways of doing another thing and we can not do both at the same time, then there are \(A+B\) ways to choose one of the actions.”
Example. Store number 1 has three different computers for sale, store number 2 has five different computers for sale and store number 3 has four different computers for sale of which one is the same as in store number 1. How many different computers are there to choose from?
Applying the addition principle, there are 3 + 5 + (4 - 1) = 11 computers to choose from, since one of them is sold in two different stores.
EXERCISE 2. Three digit password
You have forgotten your three digit password but you know that the digits of the password are capital letters and at most (no more than) one of them is a vowel.
The numbers of Finnish vowels is 8 (A-E-I-O-U-Y-Ä-Ö-Å) and the number of consonants is 20.
a) How many different cases are there when taking into consideration that at most one of the digits is a vowel?
b) How many different strings (ordered three digit sets) are there that matches of what you can remember about your password?
c) How many different strings are there all together?
Answers: b) 17 600
c) 21 952
Permutations#
Definition
Let A be a set of n elements. A permutation of A is any sequence of its elements, where every element of A appears exactly once.
In short, a permutation is an ordered arrangement of things, where the order of selection matters.
Example. Let A = {a, b, c}. All the permutations of A are {a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b} and {c, b, a}.
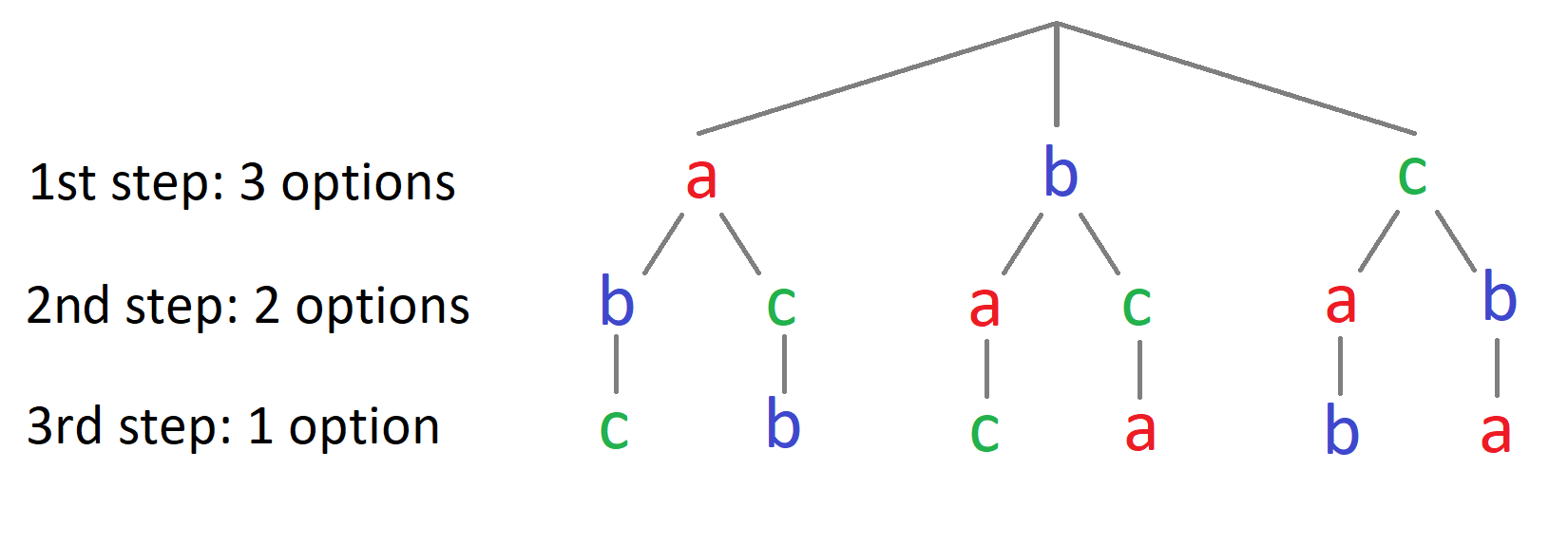
Fig. 19 The number of permutations of a set {a, b, c} can be computed from the tree moddel. In the first step we have 3 options, in the second step we have 2 options and in the last step only one choice is possible for each sequence. The total number of permutations can be computed using the multiplication principle: \(3 \cdot 2 \cdot 1 = 6\).#
Even words are permuations of a set of letters but only some sequences, or anagrams, bear signifance. For example, from letters A, C and R we can form sequences of ARC and CAR and all the other arrangements are abbreviations of some sort.
Let’s denote the number of elements in a set by n.
In general, when \(n \ge 0\), the first element can be any of the elements so there are \(n\) ways of choosing the first element (step 1).
After that there are \(n-1\) elements left, so the second element can be chosen by \(n-1\) ways (step 2).
The third element can be chosen by \(n-2\) ways and so forth, until the last element remains and there is only one way of choosing it (last step).
According to the multiplication rule, the number of permutations is \(n \cdot (n-1) \cdot (n-2) \cdot \dots \cdot 3 \cdot 2 \cdot 1=n!\), where \(n!\) is known as the factorial.
When \(n=0\), the only set with zero elements is the empty set, \(\emptyset\). The only permutation of the empty set is an empty arrangement \({}\), so it has been agreed that \(0!=1\).
Definition
In a set with a finite number of elements, the number of ordered arrangements, or permutations, is denoted by \(n!\).
EXERCISE 3. Arrangement of books on a book shelf
A teacher has a collection of 12 STEM textbooks: 3 on Physics, 4 on Chemistry and 5 on Maths.
a) How many different arrangements can be made from the textbooks?
b) How many different arrangements can be made from the textbooks, when every field of a study is arranged on its own?
Answers: a) 479 001 600
b) 103 680
Variations, the k-permutations of n#
Definition
Let A be a set of n elements and \(k<n\). A variation or a k-permutation of A is any ordered subset of A with k elements.
In short, it refers to the number of ways you can choose and arrange k elements from a set of n distinct elements, where again the order of selection matters. This is often denoted as \(P(n,k)=n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n-k+1)\), where \(P(n,k)\) consists of k factors.
The number of variations doesn’t take into consideration the factors after \((n-k+1)\). Since factors \((n-k)\cdot(n-k-1)\cdot(n-k-2)\cdot \ldots \cdot 2 \cdot 1=(n-k)!\) are reduced, the formula for the number variations is given by
\(P(n,k)=\frac{n!}{(n - k)!}\)
Example. Let A = {a, b, c}. All the varations of A with two elements are {a, b}, {a, c}, {b, a}, {b, c}, {c, a} and {c, b}.
The first letter can be chosen from 3 different letters and after that the second can be chosen from 2 different letters. According to the multiplication rule, the number of variations is \(3 \cdot 2=6\).
Using the formula we get
\(P(3,2)=\frac{3!}{(3 - 2)!}=\frac{3*2*1}{1}=6\).
EXERCISE 4. A smaller arrangement of books on a book shelf
A teacher still has a collection of 12 STEM textbooks: 3 on Physics, 4 on Chemistry and 5 on Maths. Only seven books can be fitted in the book shelf.
a) How many different arrangements can be made from the textbooks?
b) How many different arrangements can be made from the textbooks, when only two fields of a study are chosen and arranged on their own?
Answers: a) 3 991 680
b) 14 688
Combinations, the k-combinations of n (a bit unfinished)#
Definition
Let A be a set of n elements and \(0 \le k \le n\). A combination of A is any subset of A with k elements.
Since a combination is a subset of a set, the order is not significant. Let’s examine a set of A = {a, b, c}.
For a subset of 3 elements the set {a, b, c} is the same as {a, c, b} - 1 combination
For a subset of 2 elements we have sets {a, b}, {b, c}, {a, c} - 3 possible combinations
For a subset of 1 element we have sets {a}, {b}, {c} - 3 possible combinations
For a subset of 0 elements we have only empty set denoted by {} or \(\emptyset\) - 1 combination
In total, the number of all possible combinations for a set of A = {a, b, c} is 8.
The number of combinations can be computed using the formula denoted by \(\binom{n}{k}\) (read as “n over k”) also known as the Binomial coefficients. Since combinations don’t consider the order, the arrangements that result in the same combination are to be eliminated. For every combination of \(k\) items, there are \(k!\) ways to arrange those \(k\) items. Therefore,
\(C(n,k)=\binom{n}{k}=\frac{P(n,k)}{P(k,k)}=\frac{\frac{n!}{(n - k)!}}{k!}=\frac{n!}{(n - k)!k!}\)
EXERCISE 5. Two referees
A group of 12 students are having a match of Finnish baseball.
a) Two referees are needed. How many different ways there are of choosing two referees?
b) How many different ways there are of choosing one referee and one spectator?
Answers: a) 66
b) 132
EXERCISE 6. Lottery
There are 40 numbers in Finnish Lottery (there used to be 39 in the 80’s!) and 7 are chosen for one row. In Lottery draw, 7 numbers are randomly drawn plus one extra number.
a) What is the number of ways of choosing a Lottery row?
b) What is the number of Lottery rows, where there are exactly 5 correct numbers and no correct extra numbers?
Hint: How many combinations are of 5 correct numbers and how many combinations there are of numbers, that were not drawn at all?
Answers: a) 18 643 560
b) 10 416
