Juurilausekkeet

Juuret liittyvät läheisesti potensseihin. Hyvin monessa sovelluksessa pärjää toisella juurella eli neliöjuurella, tai kolmannella juurella eli kuutiojuurella. Juurta voi ajatella potenssilaskun kantalukuna. Esimerkiksi luvun 81 neliöjuuri saadaan päättelemällä: mikä luku pitää korottaa potenssiin 2, jotta saadaan 81? Luku 9 täyttää tämän ehdon. Vastaavasti luvun 8 kolmas juuri eli kuutiojuuri on 2, sillä \(2^3=8\).

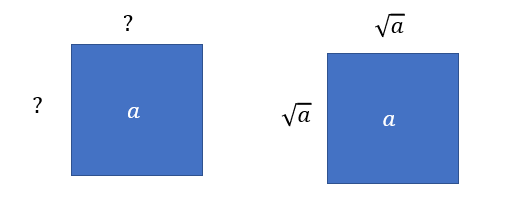
Juurilausekkeiden laskusääntöjä tarvitaan samanlaisissa tilanteissa kuin potenssilukujen laskusääntöjä: lausekkeiden sieventämisessä ja yleisten, tiettyihin lukuarvoihin sitomattomien, ongelmien ratkaisussa. Geometrisesti neliöjuuri vastaa kysymykseen: jos tiedetään neliön pinta-ala \(a\), niin mikä on neliön sivun pituus?

Määritelmä

• Luvun \(a\) neliöjuurella \(\sqrt{a}\) tarkoitetaan lukua, jolle pätee \(\sqrt{a} \geq 0\) ja \((\sqrt{a})^2=a\).

Esim. Luvun 9 neliöjuuri \(\sqrt{9}\) on 3, sillä \(3\geq 0\) ja \(3^2=9\). Myös luvulle -3 pätee ehto \((-3)^2=9\), mutta koska \(-3 < 0\), niin -3 ei ole \(\sqrt{9}\).

• Luvun \(b\) kuutiojuurella \(\sqrt[3]{b}\) tarkoitetaan lukua, jolla pätee \((\sqrt[3]{b})^3 = b\). Luvun ei tarvitse olla positiivinen.

Esim. Luvun 64 kuutiojuuri \(\sqrt[3]{64}\) on 4, sillä \(4^3=64\).

Esim. Luvun 0.001 kuutiojuuri \(\sqrt[3]{0.001}\) on 0.1, sillä \(0.1^3=0.001\).

Läheskään kaikkien lukujen neliö- tai kuutiojuuri ei ole kokonaisluku, ja tällöin sitä merkitään vain juurimerkillä. Esimerkiksi luvun 10 neliöjuuri on \(\sqrt{10}\). Laskimella sille voidaan laskea likiarvo, esimerkiksi WolframAlpha-laskin antaa likiarvoksi noin \(3.16227...\). Laskuissa käytetään mahdollisimman pitkälle mieluummin tarkkoja arvoja, sillä tällöin saadaan tarkempi lopputulos vähemmällä työllä!

Yleinen juuri

• Yleinen juuri \(\sqrt[n]{c}\) määritellään parillisille luvuille \(n\) vastaavasti kuin neliöjuuri: se on positiivinen luku, joka potenssiin \(n\) korottamalla saadaan luku \(c\). Luvun \(c\) pitää olla suurempi tai yhtä suuri kuin nolla.

Esim. Luvun 16 neljäs juuri \(\sqrt[4]{16}\) on 2, sillä \(2^4=16\). Myös luvulle -2 pätee \((-2)^4=16\), mutta koska \(-2<0\), niin -2 ei ole \(\sqrt[4]{16}\).

Esim. Luvun -49 kuudetta juurta \(\sqrt[6]{-49}\) ei ole olemassa, sillä \(-49<0\). Ei ole olemassa reaalilukua, joka potenssiin 6 korottamalla saataisiin luku -49. (Kompleksilukujen joukosta tällainen luku voidaan kuitenkin löytää, mutta niitä ei käsitellä tällä opintojaksolla.)

• Yleinen juuri \(\sqrt[n]{c}\) määritellään parittomille luvuille n vastaavasti kuin kuutiojuuri: se on mikä tahansa luku, joka potenssiin \(n\) korottamalla saadaan luku \(c\). Myös luku \(c\) voi olla positiivinen tai negatiivinen.

Esim. Luvun -32 viides juuri \(\sqrt[5]{-32}\) on -2, sillä \((-2)^5=-32\).

Laskusäännöt

Juurilausekkeille pätevät laskusäännöt, jotka seuraavassa on esitetty neliö- ja kuutiojuurille:

1. Juurten tulo on tulon juuri: \(\sqrt{a}\sqrt{b}=\sqrt{ab}\) ja \(\sqrt[3]{a}\sqrt[3]{b}=\sqrt[3]{ab}\)

Esim. Tulo \(\sqrt{27}\sqrt{3}\) voidaan laskea kahdella tavalla:

\(\sqrt{27}\sqrt{3} \approx 5.196\cdot 1.732 approx 8.999\) tai \(\sqrt{27}\sqrt{3} =\sqrt{27\cdot 3}=\sqrt{81}=9\).

Esim. Tulo \(\sqrt[3]{25}\sqrt[3]{5}\) voidaan laskea kahdella tavalla:

\(\sqrt[3]{25}\sqrt[3]{5} \approx 2.924 \cdot 1.710 approx 5.000\) tai \(\sqrt[3]{25}\sqrt[3]{5} =\sqrt[3]{25\cdot 5}=\sqrt[3]{125}=5\).

Lisäksi jos \(x>0\) ja \(m \neq 0\), niin \(\sqrt{x^m}=x^{\frac{m}{2}}\), eli toisin sanoen luvun potenssin saa ulos neliöjuuresta jakamalla eksponentin kahdella. Esimerkiksi \(\sqrt{x^6}=x^3\), jos \(x > 0\).

Esimerkki

Sievennä lauseke \(\sqrt{x^3}\sqrt{x^5}\), missä \(x > 0\).

Ratkaisu

Yhdistetään juurten tulo yhdeksi juureksi:

\(\sqrt{x^3}\sqrt{x^5}=\sqrt{x^3\cdot x^5}\).

Potenssilukujen laskusääntöjen perusteella

\(\sqrt{x^3\cdot x^5} = \sqrt{x^8}\).

Nyt voidaan ratkaisu jo päätellä: kysytty juuri on se luku, joka potenssiin 2 korotettuna tuottaa luvun \(x^8\), siis \(x^4\).

2. Osamäärän juuri on juurten osamäärä: \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) ja \(\sqrt[3]{\frac{a}{b}}=\frac{\sqrt[3]{a}}{\sqrt[3]{b}}\)

Esim.

Jakolasku \(\frac{\sqrt{810}}{\sqrt{10}}\) voidaan laskea vaikka päässälaskuna hyödyntämällä sääntöä \(\frac{\sqrt{810}}{\sqrt{10}}=\sqrt{\frac{810}{10}}=\sqrt{81}=9\).

Sääntöä voidaan käyttää myös seuraavasti: \(\sqrt[3]{\frac{27}{64}}=\frac{\sqrt[3]{27}}{\sqrt[3]{64}}=\frac{3}{4}\).

Esimerkki

Sievennä lauseke \(\frac{\sqrt{x^3}}{\sqrt{x}}\), jossa \(x > 0\).

Ratkaisu

Yhdistetään osamäärä yhdeksi juurilausekkeeksi:

\(\frac{\sqrt{x^3}}{\sqrt{x}}=\sqrt{\frac{x^3}{x}}\).

Potenssilukujen laskusääntöjen perusteella

\(\sqrt{\frac{x^3}{x}}=\sqrt{x^2}\)

ja edelleen neliöjuuren määritelmän perusteella vastaukseksi tulee \(x\).

Murtopotenssiesitys

Mitä tahansa juurta voidaan merkitä \(\sqrt[n]{c}=c^{\frac{1}{n}}\). Tätä kutsutaan murtopotenssiesitykseksi. Merkinnän avulla juurilausekkeita päästään käsittelemään potenssien laskusääntöjen avulla. Murtopotenssiesitys on hyödyllinen, jos halutaan sieventää lauseke, jossa on mukana sekä juuria että potensseja, tai sekä neliö- että kuutiojuuria.

WolframAlpha ja monet muut työkalut ymmärtävät murtopotenssimerkintöjä. Esimerkiksi kuutiojuuri luvusta 100 voidaan WolframAlphassa laskea näppärästi komennolla “100^(1/3)”. Toinen vaihtoehto olisi kirjoittaa “cubic root of 100” tai “cbrt(100)”.

Esimerkki

Sievennä lauseke \(x \cdot \sqrt{x}\), missä \(x > 0\).

Ratkaisu

\(x \cdot \sqrt{x}=x\cdot x^{\frac{1}{2}}=x^1 \cdot x^{\frac{1}{2}}=x^{1+\frac{1}{2}}=x^{\frac{3}{2}}\)

Esimerkki

Sievennä lauseke \(\sqrt[3]{x}\cdot \sqrt{x}\), missä \(x > 0\).

Ratkaisu

\(\sqrt[3]{x}\cdot \sqrt{x}=x^{\frac{1}{3}}\cdot x^{\frac{1}{2}}=x^{\frac{1}{3}+\frac{1}{2}}=x^{\frac{2}{6}+\frac{3}{6}}=x^{\frac{5}{6}}\)

Pohdittavaksi

Neliöstä lohkaistaan pienempi neliö, jonka pinta-ala on \(\frac{1}{8}\) alkuperäisestä pinta-alasta. Kuinka suuri on pienemmän neliön sivun pituus verrattuna alkuperäiseen?

Ratkaisu

Merkitään neliön alkuperäistä pinta-alaa \(A\). Tällöin alkuperäinen sivun pituus on \(x=\sqrt{A}\). Uusi pinta-ala on \(\frac{A}{8}\). Uuden sivun pituus on \(\sqrt{\frac{A}{8}}=\frac{\sqrt{A}}{\sqrt{8}}=\frac{\sqrt{A}}{2.83}=\frac{1}{2.83} x\). Sivu on siis noin \(\frac{1}{2.83} x = 0.35 x\).

Pohdittavaksi

Tuulivoimalan tuottama sähköteho on fysiikan lakien mukaisesti verrannollinen tuulen nopeuden kolmanteen potenssiin. Kuinka paljon tuulen nopeuden pitäisi kasvaa, jotta tuulivoimalan teho kaksinkertaistuisi?

Ratkaisu

Merkitään alkuperäistä tehoa \(P=kv_1^3\), missä \(k\) on verrannollisuuskerroin ja \(v_1\) alkuperäinen tuulen nopeus. Uusi teho on \(2P=kv_2^3\), missä \(v_2\) on tämän tehon saavuttamiseksi tarvittava tuulen nopeus. Näistä saadaan yhtälö \(2 kv_1^3=kv_2^3\), josta on mahdollista ratkaista \(v_2=\sqrt[3]{2v_1^3}=\sqrt[3]{2}v_1 = 1.26 v_1\). Tuulen nopeuden pitäisi kasvaa vain 26 % alkuperäisestä.