Pallo

Asumme suunnilleen pallon muotoisen planeetan pinnalla. Avaruuden kappaleet, joilla on tarpeeksi paljon massaa, muovautuvat itsekseen pallon muotoisiksi. Pallon muotoa hyödynnetään myös esimerkiksi sääluotaimisissa, erilaisissa säiliöissä ja jopa asumuksissa (igluissa).

Pallon määrittää sen säde \(r\). Pallopinta muodostuu pisteistä, jotka ovat säteen etäisyydellä pallon keskipisteestä.

Pallon tilavuus on \(V=\frac{4}{3} \pi r^3\) ja pinta-ala \(A=4 \pi r^2\).

Perustelu

Pallon tilavuuden kaava voidaan johtaa samaan tapaan kuin kartion tilavuuden kaava, siis “sahaamalla” pallo äärettömään moneen äärettömään ohueen siivuun ja laskemalla sitten näiden siivujen tilavuudet yhteen. Näiden siivujen tilavuuden summan laskemiseksi tarvitaan integraalilaskentaa, joka ei kuulu tähän opintojaksoon. Tässä eräs vaihtoehtoinen todistus, joka ei vaadi integraalilaskentaa.

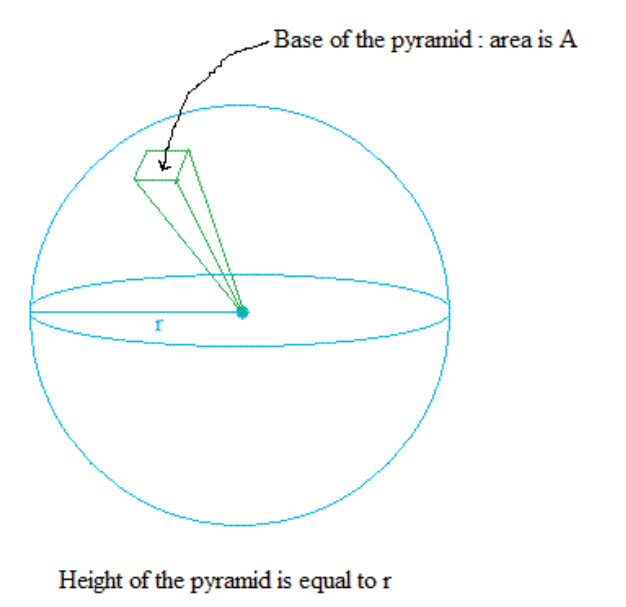
Jos pallon tilavuus \(V=\frac{4}{3}\pi r^3\) uskotaan todeksi, niin sen avulla voidaan johtaa pallon pinta-alan \(A\) laskukaava. Ajatellaan, että pallo muodostuu \(n\) kappaleesta kuvan mukaisia kartioita, joiden pohjan ala on \(A_k\) ja joiden korkeus on sama kuin pallon säde eli \(r\). Kartion tilavuudeksi tiedetään \(V_k=\frac{1}{3}A_k r\).

Määritellään aputuloksena kartion pohjan alan ja tilavuuden suhde: \(\frac{A_k}{V_k}=\frac{A_k}{\frac{1}{3} A_k r}=\frac{3}{r}\).

Koko pallon tilavuus on sama kuin kaikkien kartioiden tilavuus, siis \(V=n V_k = n \frac{1}{3} A_k r\). Toisaalta tiedetään, että pallon pinta-ala koostuu \(n\) kappaleesta kartioiden pohjien aloja \(A_k\).

Kirjoitetaan nyt pallon pinta-alan ja pallon tilavuuden suhde:

\(\frac{A}{V} = \frac{n A_k}{n V_k} = \frac{A_k}{V_k}=\frac{3}{r}\)

Toisin sanoen

\(A=\frac{3}{r}\cdot V = \frac{3}{r} \cdot \frac{4}{3} \pi r^3 = 4\pi r^2\).

Esimerkki

Pallon A pinta-ala on \(2400~\text{cm}^2\) ja pallon B tilavuus on \(9200~\text{cm}^3\). Kumpi palloista on suurempi?

Ratkaisu

Kirjoitetaan ja ratkaistaan yhtälöt, joissa tuntemattomina ovat pallojen säteet \(r_A\) ja \(r_B\):

\(2400~\text{cm}^2=4 \pi r_A^2 \leftrightarrow r_A=\sqrt{\frac{2400~\text{cm}^2}{4\pi}}\approx 13.8~\text{cm}\)

\(9200~\text{cm}^2=\frac{4}{3} \pi r_B^3 \leftrightarrow r_B=\sqrt[3]{\frac{3\cdot 9200~\text{cm}^3}{4\pi}}\approx 13.0~\text{cm}\)

Vastaus: Pallon A säde on noin 13.8 cm ja pallon B säde on noin 13.0 cm, joten pallo A on suurempi.

Esimerkki

Pihallasi on suunnilleen pallon muotoinen kivi. Haluaisit siirtää kiven ja arvioit, jaksaako sen siirtää vierittämällä. Mittaat kiven ympärysmitaksi leveimmältä kohdalta 180 cm. Selvität netistä, että kivilajin tiheys on keskimäärin noin 3000 kiloa kuutiometriä kohden. Paljonko kiven massa on? Massa on tiheyden ja tilavuuden tulo.

Ratkaisu

Leveimmältä kohdalta pallon poikkileikkaus on ympyrä, jonka säde on sama kuin pallon säde. Ympärysmittaa \(p\) ja sädettä yhdistää kaava \(p=2\pi r\), joten pallon säde on $r=\frac{p}{2 \pi}. Sijoitetaan säde tilavuuden kaavaan:

\(V=\frac{4}{3}\pi r^3 = \frac{4}{3} \pi \left(\frac{p}{2 \pi}\right)^3\)

Sijoitetaan mitattu ympärysmitta yhtälöön. Koska tiheys on annettu kuutiometriä kohden, ympärysmitan pitää olla yksikössä metri.

\(V=\frac{4}{3} \pi \left(\frac{1.80~\text{m}}{2 \pi}\right)^3\approx 0.0985~\text{m}^3\)

Massa on \(3000~\frac{~text{kg}}{\text{m}^3}\cdot 0.0985~\text{m}^3 \approx 296~\text{kg}\).

Esimerkki

Maan säde on noin 6380 km ja Kuun säde noin 1737 km. Vertaa Maan ja Kuun pinta-alaa ja tilavuutta.

Ratkaisu

Vertailu onnistuisi laskemalla Maan ja Kuun pinta-ala ja tilavuus ja sitten niiden suhteet. Toinen tapa on tarkastella pinta-alan ja tilavuuden laskukaavoja. Merkitään Maan sädettä \(r_M\), pinta-alaa \(A_M\) ja tilavuutta \(V_M\), ja Kuun sädettä \(r_K\), pinta-alaa \(A_K\) ja tilavuutta \(V_k\).

Pinta-alojen suhde on

\(\frac{A_M}{A_K}=\frac{4\pi r_M^2}{4 \pi r_K^2}\),

joka voidaan sieventää muotoon

\(\frac{r_M^2}{r_K^2}\)

ja edelleen

\(\left\frac{r_M}{r_K}\right)^2\)

ja lukuarvot sijoittamalla saadaan suhteeksi

\(\left(\frac{1737}{6380}\right)^2\approx 13.5\)

(yksikötkin supistuvat laskussa pois). Maan pinta-ala on siis 13.5 kertaa Kuun pinta-alaan verrattuna.

Vastaavasti tilavuuksien suhde

\(\frac{V_M}{V_K}=\frac{\frac{4}{3}\pi r_M^3}{\frac{4}{3} \pi r_K^3}\)

sievenee muotoon

\(\left\frac{r_M}{r_K}\right)^3\) eli \(\left(\frac{1737}{6380}\right)^2\approx 50\).

Harvemmin käytettyjä palloon liittyviä laskukaavoja ovat esim. pallokalotin alan ja tilavuuden kaava. Tällaisilla kaavoilla voidaan arvioida vaikkapa sitä, kuinka suuri alue maapallolla on pohjoisen napapiirin pohjoispuolella. Kalotti saadaan aikaan, kun pallo leikataan kahteen palaan. Kalotin korkeus \(h\) on kohtisuora matka tämän leikkauspinnan keskeltä pallon säteen etäisyydelle. Pallon segmentti tarkoittaa pallokalotin sisäpuolelle jäävää osuutta pallosta (eli kalotti on ikään kuin hattu ja segmentti on se osa päästä, joka jää hatun suojaan). Kaavojen perusteluja löytyy esimerkiksi Wikipediasta.

• Pallokalotin ala: \(A= 2 \pi r h\)

• Pallosegmentin tilavuus: \(V=\pi h^2 \left(r-\left(\frac{h}{3}\right)\right)\)