Sinifunktio#
Monet luonnossa ja laboratoriossa esiintyvät ilmiöt noudattavat ainakin likimäärin sinifunktiota. Sinifunktion kuvaaja on aaltomainen. Toisin sanoen funktion kuvaama suure vaihtelee toistuvasti minimi- ja maksimiarvojensa välillä. Muuttujana sinifunktiossa on yleensä kirjaimen \(x\) sijasta \(t\), joka viittaa aikaan (time). Esimerkiksi veden korkeus satamassa nousu- ja laskuveden vaihdellessa noudattaa sinifunktiota. Toinen esimerkki on pistorasiasta saatava vaihtovirta. Sähkövirran voimakkuus vaihtelee hyvin nopeasti, kunnes virta kulkee muuntajan läpi esimerkiksi tietokoneen virtalähteeseen.
Sinifunktion parametrit#
Yleinen sinifunktio on muotoa \(f(t)=A\sin{(\omega t-\phi)}+B\). Funktiot parametrit ovat seuraavat:
funktion arvon keskiarvo on \(B\)
amplitudi \(A\) kertoo funktion minimi- ja maksimipoikkeaman funktion keskiarvosta \(B\)
kulmataajuudesta \(\omega\) voidaan laskea, kuinka tiheästi funktion huippukohdat toistuvat
vaihe-ero \(\phi\) kuvaa sitä, kuinka paljon funktio poikkeaa vaakasuunnassa funktiosta \(\sin{\omega t}\)
Maksimikohtien (tai minimikohtien) välistä aikaa sanotaan funktion aallonpituudeksi \(\lambda\), ja se on yhteydessä kulmataajuuden yhtälön \(\lambda=\frac{2\pi}{\omega}\) mukaisesti.
Sinifunktion maksimiarvo saavutetaan, kun \(\sin{(\omega t-\phi)}=1\), sillä sinifunktio voi saada arvoja vain lukujen -1 ja 1 väliltä. Yksikköympyrältä voidaan päätellä, että arvo 1 saavutetaan, kun \(\omega t-\phi = \frac{\pi}{2}\). Tästä voidaan ratkaista yhden ajanhetken \(t\), jolloin funktio saa suurimman arvonsa. Muut huippuarvot seuraavat aallonpituuden välein tästä hetkestä. Vastaavasti minimiarvoja saavutetaan silloin, kun \(\omega t -\phi = -\frac{\pi}{2}\).
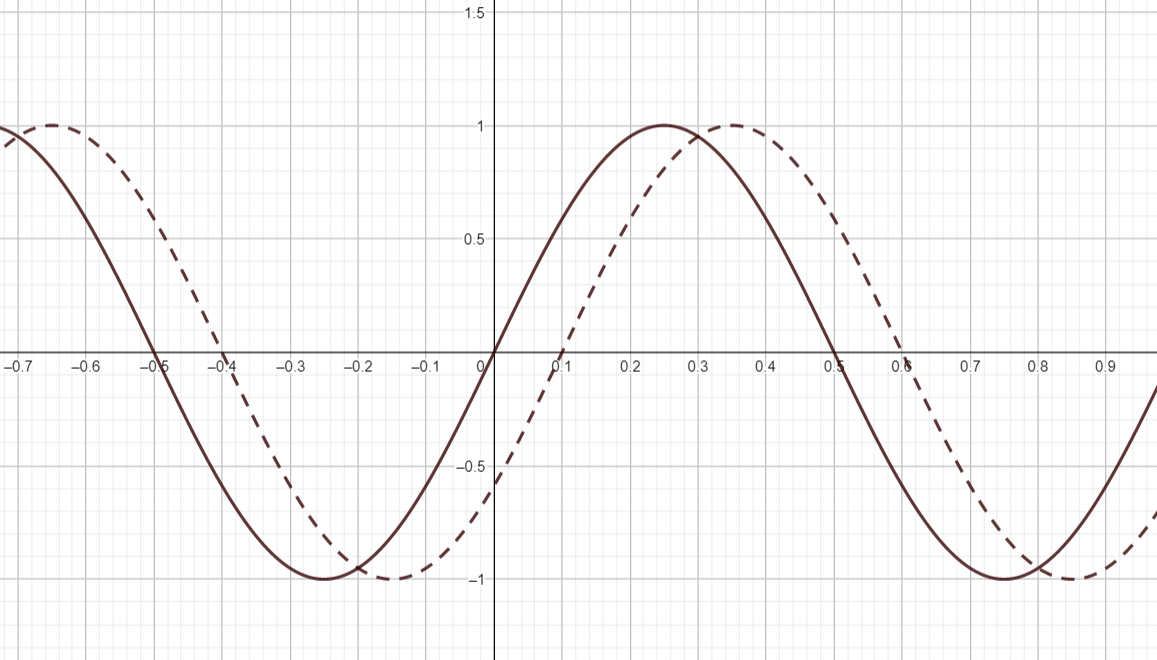
Vaihesiirto \(\phi\) ei suoraan tarkoita sitä, kuinka paljon funktion kuvaaja on vaakasuunnassa siirtynyt aika-akselin yksiköissä mitattuna. Alla olevan kuvan esimerkissä katkoviivalla piirretty käyrä \(g(t)\) tulee ajan \(T=0.1\) verran mustalla viivalla piirrettyä funktiota \(f(t)\) jäljessä. Kummankin käyrän huippukohtien välinen aika on \(\lambda=1\), joten kulmataajuus on kummallakin sinikäyrällä \(\omega=\frac{2\pi}{1}=2\pi\). Vaihesiirto saadaan laskettua yhtälöstä \(T=\frac{\phi}{\omega}\). Tässä esimerkissä vaihe-ero on siis \(\phi=\omega T = 2\pi \cdot 0.1 = 0.2 \pi = \frac{\pi}{5}\). Lisäksi vielä nähdään, että kummankin funktion keskiarvo on \(0\) ja amplitudi \(1\). Funktioiden lausekkeiksi saadaan siis \(f(t)=\sin{(2\pi t)}\) ja \(g(t)=\sin{(2\pi t -\frac{\pi}{5})}\).
Esimerkki
Muodosta lauseke funktiolle \(f(t)=A\sin{(\omega t-\phi)}+B\), kun tiedetään, että funktion aallonpituus on 6, eräs maksimiarvo on 3 hetkellä \(t=2\), ja minimiarvo on -1.
Ratkaisu
\(B\) saadaan laskemalla funktion maksimi- ja minimiarvojen keskiarvo: \(B=\frac{3+(−1)}{2} = 1\).
\(A\) on suurin poikkeama keskiarvosta: \(A=3−1=2\) tai \(A=1-(-1)=2\).
Koska aallonpituus on \(\lambda = \frac{2\pi}{\omega}\), niin kulmataajuus on \(\omega=\frac{2\pi}{\lambda}=\frac{2\pi}{6}=\frac{\pi}{3}\).
Koska eräs sinifunktion maksimikohta esiintyy kulman arvolla \(\frac{\pi}{2}\), niin vaihe-ero voidaan ratkaista yhtälöstä \(\omega t-\phi = \frac{\pi}{2}\), siis \(\phi=\omega t -\frac{\pi}{2}\). Sijoittamalla lukuarvot saadaan \(\phi = \frac{\pi}{3}\cdot 2 -\frac{\pi}{2} = \frac{2\pi}{3}-\frac{\pi}{2}=\frac{\pi}{6}\).
Lauseke on siis \(f(t)=2\sin{(\frac{\pi}{3} t-\frac{\pi}{6})}+1\). Ratkaisun voi vielä tarkistaa piirtämällä yhtälöstä kuvaajan esimerkiksi GeoGebralla.
Esimerkki
Auringonpilkkujen määrä vaihtelee jaksollisesti. Vuosittain havaittavien auringonpilkkujen määrä noudattaa likimain sinifunktiota. Auringonpilkkuja on ollut vähimmillään yksi ja enimmillään 110 kappaletta. Maksimiarvot saavutettiin vuosina 1750 ja 1948, ja niiden välissä oli 18 jaksoa. Selvitä sinifunktion parametrit.
Ratkaisu
Funktion yleinen muoto on \(f(t)=A\sin{(\omega t-\phi)}+B\).
Aluksi voidaan selvittää keskiarvo \(B=\frac{1+110}{2}=55.5\)
Amplitudi saadaan vähentämällä keskiarvosta minimiarvo, eli \(A=55.5-1=54.5\), tai vähentämällä maksimiarvosta keskiarvo eli \(A=110-55.5=54.5.\)
Aallonpituus eli yhden jakson pituus saadaan jakamalla annettu aikaväli (1750-1948) eli 198 vuotta jaksojen määrällä:
\(\lambda=\frac{198}{18}=11\)
Tällöin kulmataajuus on \(\omega=\frac{2\pi}{\lambda}=\frac{2\pi}{11}\approx 0.57\)
Lopuksi lasketaan vaihe-ero \(\phi\) hyödyntämällä tietoa, että eräs maksimi esiintyi vuonna 1750:
\(\omega t - \phi = \frac{\pi}{2}\)
\(-\phi = \frac{\pi}{2}-\omega t\)
\(\phi=\omega t - \frac{pi}{2}\)
\(\phi=\frac{2\pi}{11}\cdot 1750 - \frac{\pi}{2}\)
\(\phi\approx 998\)
Malli on siis muotoa \(54.5~\sin{(0.57 t - 998)}+55.5\)
