Polynomit#
Algebran tehtävissä on yleensä lukujen lisäksi kirjaimia, kuten \(x\). Lukuja ja kirjaimia yhdistellään kerto- ja yhteenlaskuilla. Tällöin muodostuu matemaattinen olio, jota kutsutaan nimellä polynomi.
Tarkemmin määriteltynä polynomi on lauseke, jossa on termejä ja termien välisiä yhteenlaskuja. Polynomin termit sisältävät numerokertoimia (kerroinosa) ja kirjaimilla merkittyjä lukuja ja niiden potensseja (kirjainosa). Jokaisessa polynomin termissä kirjainosan eksponentin pitää olla vähintään nolla.
Esim. \(3x+5x^2-2x\) on polynomi, jonka termit ovat \(3x\), \(5x^2\) ja \(-2x\).
Termit ovat samanmuotoisia, jos niissä on sama kirjainosa. Niissä on sama kirjain ja sama eksponentti. Kerroinosien ei kuitenkaan tarvitse olla samat! Esimerkiksi \(-3x^2\) ja \(4x^2\) ovat samanmuotoisia, mutta \(-3x^2\) ja \(-3x\) eivät ole.
Esim. Polynomissa \(5x^4+2x^2+3x-2\) ei ole samanmuotoisia termejä.
Esim. Polynomissa \(5x^3+2x-3x^3-x\) on samanmuotoisia termejä: \(5x^3\) ja \(-3x^3\) ovat keskenään samanmuotoisia, ja \(2x\) ja \(-x\) keskenään samanmuotoisia.
Termien järjestys ja kirjainten määrä
Polynomin termit voisi periaatteessa kirjoittaa missä järjestyksessä tahansa, sillä yhteenlasku on vaihdannainen operaatio. Luvuilla esitettynä tämä tarkoittaa sitä, että lasku \(2+3\) tuottaa saman tuloksen kuin \(3+2\). Sääntö pätee myös silloin, kun laskun tulokselle ei pystytä sanomaan mitään lukuarvoa: esimerkiksi \(x+3x^2\) on sama asia kuin \(3x^2+x\). Näin ollen saman polynomin voisi kirjoittaa monella eri tavalla. Tapana on kuitenkin kirjoittaa termit laskevan eksponentin mukaiseen järjestykseen, siis mieluummin \(-5x^2+4x+1\) kuin \(1+4x-5x^2\). Viimeiseksi jätetään niinsanottu vakiotermi, eli termi jossa on pelkkä luku.
Tässä luvussa käsitellään enimmäkseen sellaisia polynomeja, joissa on vain yhtä kirjainta, esimerkiksi \(x\). Samassa polynomissa voi kyllä esiintyä esimerkiksi kirjaimia \(x\) ja \(y\), toisin sanoen lausekkeen arvo voi riippua useammasta kuin yhdestä muuttujasta. Tällaisiin tilanteisiin törmää varmasti esimerkiksi fysiikkaa opiskellessaan.
Näkymättömät kertoimet ja kirjaimet
Periaatteessa jokaisessa polynomin termissä on sekä kerroin- että kirjainosa, vaikka niitä ei aina näykään!
Jos numeroa ei näy, kerroinosa on \(1\). Esimerkiksi \(1\cdot x\) on sama asia kuin \(x\). Jos termi on \(-x\), niin kerroinosa on \(-1\).
Jos kirjainta ei näy, niin kirjainosan voisi kirjoittaa muodossa \(x^0\). Potenssilukujen laskusääntöjen mukaanhan \(x^0=1\). Yleensä kirjainosaa ei kuitenkaan tällöin kirjoiteta näkyviin, vaan kyseistä termiä voi käsitellä pelkkänä lukuna.
Kirjainosan eksponenttia \(1\) ei yleensä merkitä näkyviin, sillä mille tahansa luvulle \(a\) pätee \(a^1=a\). Niinpä esimerkiksi polynomi \(x+2\) voitaisiin esittää myös muodossa \(1\cdot x^1+2\cdot x^0\).
Lisäksi polynomin voi ajatella koostuvan pelkästään yhteenlaskuista. Jos polynomissa on termi, jossa on miinusmerkkinen kerroin, voidaan ajatella että yhteenlaskussa vain on mukana negatiivinen luku. Esimerkiksi \(3x^2-4x\) on siis sama asia kuin \(3x^2+(-4x)\).
Polynomien sieventäminen#
Polynomien sieventäminen tarkoittaa polynomin esittämistä mahdollisimman yksinkertaisessa muodossa. Sieventäminen helpottaa esimerkiksi yhtälöiden käsittelyä. Sieventäminen auttaa myös silloin, kun monimutkaisia yhtälöitä annetaan tietokoneen käsiteltäväksi.
Jokainen laskutoimitus vie aikaa
Vaativassa numeerisessa laskennassa ja data-analytiikassa lausekkeiden esitysmuoto saattaa vaikuttaa merkittävästi aikaan, joka tietokoneelta kuluu ongelman ratkaisuun. Jokainen laskutoimitushan vie tietokoneelta tietyn ajan. Esimerkiksi laskutoimitus \(2x+x\) vaatii yhden kerto- ja yhden yhteenlaskun, kun taas saman ongelman esittäminen muodossa \(3x\) vie aikaa vain yhden kertolaskun verran. Kun tietokone esimerkiksi etsii usealle muuttujalle arvoja, joilla saadaan laskutoimitukselle - esimerkiksi tehtaan valmistaman uuden tuotteen tuottamalle voitolle - suurin mahdollinen tulos, laskuun voi kulua tuntikausia. Tällöin olisi hyvä, ettei tietokone turhaan laske ylimääräisiä välivaiheita huonosti sievennetyn lausekkeen takia!
Samanmuotoisten termien yhdistäminen#
Samanmuotoisten termien kertoimet voi laskea yhteen, jolloin lauseke sieventyy huomattavasti. Samanmuotoisia termejä yhdistetään myös silloin, kun kaksi polynomia lasketaan yhteen tai vähennetään toisistaan.
Esim. Polynomien \(2x+1\) ja \(-3x^2+4x\) summa on
\(\begin{equation}\begin{split} 2x+1+(-3x^2+4x) & =2x+1-3x^2+4x \\& =(2+4)x+1-3x^2 \\ &=6x+1-3x^2\\&=3x^2+6x-1\end{split}\end{equation}\),
ja samojen polynomien erotus on
\(\begin{equation}\begin{split}2x+1-(-3x^2+4x) & =2x+1+3x^2-4x \\ & =(2-4)x+1+3x^2 \\& =-2x+1+3x^2\\&=3x^2-2x+1\end{split}\end{equation}\).
Esimerkki
Yhdistä samanmuotoiset termit:
a) \(2m-n+5m+4n\), b) \(x^2+4x-2x^2-2x\)
Ratkaisu
a) \(2m-n+5m+4n=(2+5)m+(-1+4)n=7m+3n\)
Enempää termejä ei voi yhdistellä, sillä \(7m\) ja \(3n\) eivät ole samanmuotoisia.
b) \(x^2+4x-2x^2-2x=(1-2)x^2+(4-2)x=-x^2+2x\)
Esimerkki
Laske polynomien summa tai erotus:
a) \((3x^2-5x+2)+(4x-1)\)
b) \((2x^3+x-1)-(x^2+3x-4)\)
Ratkaisu
a) \((3x^2-5x+2)+(4x-1) = \)
\( 3x^2-5x+2+4x-1= \)
\( 3x^2+(-5+4)x+(2-1) = \)
\(3x^2-x+1\)
b) \((2x^3+x-1)-(x^2+3x-4)= \)
\(2x^3+x-1-x^2-3x-(-4)=\)
\(2x^3+x-1-x^2-3x+4=\)
\(2x^3-x^2+(1-3)x+(-1+4)=\)
\(2x^3-x^2-2x-3\)
Polynomien kertolasku#
Polynomin voi kertoa luvulla tai toisella polynomilla. Luvulla kertominen on helpompaa: polynomin jokainen termi kerrotaan kyseisellä luvulla.
Esim. \(3(5x^2+4x-2)=3\cdot 5x^2+3\cdot 4x+3\cdot (-2)=15x^2+12x-6\)
Kertolasku toimii näin myös silloin, jos polynomi kerrotaan jollakin sellaisella polynomilla, jolla on vain yksi termi. Kertoimina olevat luvut kerrotaan keskenään, ja kirjainosien eksponentteja muokataan potenssilukujen kertolaskun sääntöjen mukaisesti.
Esim. \(x^2(3x^2+4x-5)=x^2\cdot 3x^2 + x^2\cdot 4x + x^2 \cdot (-5) = 3x^4+4x^3-5x^2\)
Sama sääntö toimii myös, kun polynomi jaetaan luvulla. Jakolaskun voi ajatella myös käänteisluvulla kertomisella: jos esimerkiksi polynomi pitää jakaa luvulla 4, niin polynomin jokaisen termin voi kertoa luvulla \(\frac{1}{4}\). Tällöin ainakin laskutoimituksen kirjoittaminen helpottuu!
Esim. \(\frac{x^2+8x-5}{4}=\frac{1}{4}(x^2+8x-5)=\frac{1}{4}x^2+\frac{1}{4}8x-\frac{1}{4}\cdot 5=\frac{1}{4}x^2+2x-\frac{5}{4}\)
Kun polynomi kerrotaan toisella polynomilla, jolla on useampi kuin yksi termi, tehdään kertolaskut yksitellen, ja sitten tulot lasketaan yhteen. Laskut voi suorittaa monessa eri järjestyksessä. Apuna voi käyttää esimerkiksi seuraavanlaista kuviota:
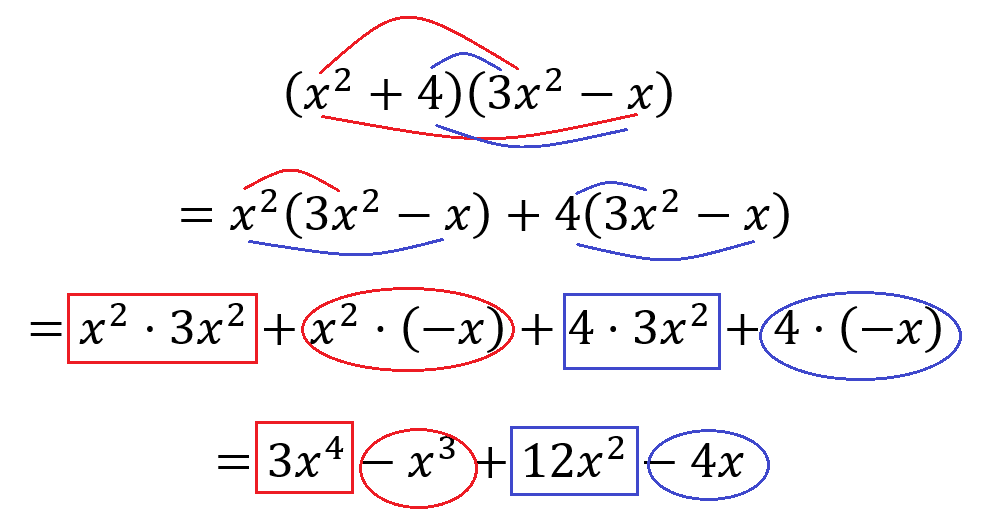
Esim. \((\mathbf{x}+\mathbf{2})(x^2+1)=\mathbf{x}(x^2+1)+\mathbf{2}(x^2+1)=\)
\(\mathbf{x}\cdot x^2+\mathbf{x}\cdot 1+\mathbf{2}\cdot x^2+\mathbf{2}\cdot 1=x^3+x+2x^2+2\)
Esim. \((x+y)(3+z)=3x+xz+3y+yz\)
Esim. \((x-2)(y+1)=xy+x\cdot 1-2y-2 = xy+x-2y-2\)
Graafinen apu kertolaskuun
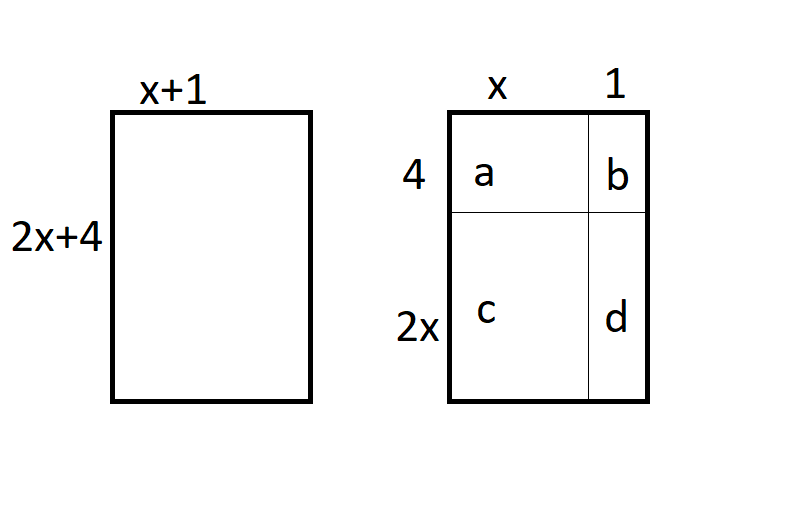
Esimerkiksi kertolasku \((x+1)(2x+4)\) on helppo hahmottaa seuraavan kuvan avulla. Piirretään suorakulmio, jonka toisen sivun pituus on \(x+1\) ja toisen sivun pituus on \(2x+4\). Suorakulmion pinta-ala on tunnetusti sivujen pituuksien tulo. Toisaalta pinta-ala voidaan hahmottaa myös jakamalla toinen sivu osiin \(x\) ja \(1\), ja toinen sivu osiin \(2x\) ja \(4\). Tällöin alueen pinta-ala saadaan, kun lasketaan palasten alat erikseen ja sitten summataan ne.
Kuvassa alueen \(a\) pinta-ala on \(4\cdot x = 4x\), alueen \(b\) pinta-ala on \(4\cdot 1 = 4\), alueen \(c\) pinta-ala on \(2x\cdot x = 2x^2\) ja alueen \(d\) pinta-ala on \(2x\cdot 1 = 2x\). Yhteensä pinta-ala on siis \(4x+4+2x^2+2x=2x^2+6x+4\).
Esimerkki
Suorakulmion muotoisen alueen sivujen pituudet ovat \(x\) metriä ja \(3x\) metriä. Kuinka paljon alueen pinta-ala kasvaa, kun lyhyttä sivua kasvataan yhdellä metrillä ja pitkää sivua viidellä metrillä? Entä paljonko alueen ympärysmitta kasvaa?
Ratkaisu
Tässä ongelmassa tarvitaan polynomien laskusääntöjä, mutta myös potenssilaskusääntöjä!
Aluksi suorakulmion pinta-ala on \(x\cdot 3x=3x^2\) neliömetriä. Laajennuksen jälkeen ala on \((x+1)(3x+5)=3x^2+5x+3x+5\) neliömetriä. Sievennetään lauseke yhdistämällä samanmuotoiset termit: \(3x^2+5x+3x+5=3x^2+8x+5\). Alan muutos saadaan, kun vähennetään uudesta pinta-alasta vanha pinta-ala. Muutos on siis \(3x^2+8x+5-3x^2=8x+5\) neliömetriä.
Lasketaan vielä alkuperäinen ja uusi ympärysmitta. Ympärysmitta koostuu kahdesta lyhyestä ja kahdesta pitkä sivusta. Siis aluksi ympärysmitta on \(2x+2\cdot 3x=2x+6x=8x\) metriä, ja uusi ympärysmitta on \(2(x+1)+2(3x+5)=2x+2+6x+10=8x+12\) metriä. Muutos on \(8x+12-8x=12\) metriä. Tämän olisi toki voinut päätellä suoraankin laskemalla yhteen tehtävässä annetut sivujen pituuksien muutokset.
Binomikaavat
Polynomien kertolaskun erikoistapauksina saadaan kolme muistisääntöä, ns. binomikaavat:
Summan neliö: \((a+b)^2=a^2+2ab+b^2\)
Erotuksen neliö: \((a-b)^2=a^2-2ab+b^2\)
Summan ja erotuksen tulo: \((a+b)(a-b)=a^2-b^2\)
Kaavoissa a ja b voivat olla lukuja, kirjaimia tai lausekkeita.
Binomikaavojen perustelu
Binomikaavat voidaan perustella suoraan laskemalla.
Summan neliö:
\((a+b)^2=(a+b)(a+b)= \)
\(a(a+b)+b(a+b)=a^2+ab+ba+b^2=a^2+2ab+b^2\)
Erotuksen neliö:
\((a-b)^2=(a-b)(a-b)= \)
\( a(a-b)-b(a-b)=a^2-ab-ab+b^2=a^2-2ab+b^2\)
Summan ja erotuksen tulo:
\((a+b)(a-b)=a(a-b)+b(a-b)=a^2-ab+ab-b^2=a^2-b^2\)
Esimerkki
Sievennä binomikaavojen avulla:
a) \((x+3)^2\)
b) \((x+5)(x-5)\)
c) \((3x+1)^2\)
d) \((x-3)^2\)
Ratkaisu
a) \((x+3)^2=x^2+2\cdot x \cdot 3+3^2=x^2+6x+9\)
b) \((x+5)(x-5)=x^2-5^2=x^2-25\)
c) \((3x+1)^2=(3x)^2+2\cdot 3x\cdot 1+1^2=9x^2+6x+1\)
d) \((x-3)^2=x^2-2\cdot x \cdot 3+3^2=x^2-6x+9\)
Binomikaavojen käyttö takaperin
Binomikaavoja voi käyttää myös toiseen suuntaan, eli muuttamaan polynomin joko summan tai erotuksen neliöksi, tai summan ja erotuksen tuloksi. Tätä tarvitaan esimerkiksi silloin, kun johdetaan ratkaisukaava toisen asteen yhtälölle.
Geometriassa taas on joskus tarvetta esittää muotoja yhtälöinä. Esimerkiksi ympyrä, jonka keskipiste on \(xy\)-koordinaatiston piste \((x_0,y_0)\) ja säde \(r\), voidaan esittää muodossa \((x-x_0)^2+(y-y_0)^2=r^2\). Binomikaavoja takaperin hyödyntämällä voidaan esimerkiksi huomata, että yhtälö \(x^2 - 6 x + y^2 - 8 y = 0\) esittää ympyrää, jonka keskipiste on (3,4) ja säde 5.
Yhteisen tekijän erottaminen#
Usein on hyödyllistä muuttaa polynomi kertolaskuksi. Tällöin sanotaan, että polynomi on tulomuodossa. Tällaista muunnosta varten polynomille pitää etsiä yhteinen tekijä eli kerroin, joka koskee kaikkia polynomin termejä. Yhteinen tekijä voi olla luku, kirjain tai monimutkaisempi lauseke. Yhteinen tekijä voi olla jokin seuraavista:
lukua 1 suurempi kerroin, jolla polynomin jokainen termi on jaollinen
kirjain, joka esiintyy jokaisessa polynomin termissä, korotettuna pienintä polynomissa esiintyvää eksponenttia vastaavaan potenssiin
edellisten yhdistelmä.
Joskus polynomissa ei ole sellaista lukua tai kirjainta, joka täyttäisi minkään edellisistä ehdoista. Tällaisetkin polynomit voidaan usein esittää kertolaskuna hyödyntämällä polynomin nollakohtia, eli niitä lukuja, jotka \(x\):n paikalle sijoitettuna tuottavat polynomin arvoksi 0. Tällaisin tapauksiin palataan toisen asteen polynomifunktioiden yhteydessä.
Kun yhteinen tekijä on tunnistettu, se erotetaan kertoimeksi koko polynomin eteen, ja polynomi kirjoitetaan perään suluissa ilman yhteistä tekijää. Suluissa olevan osan saa muodostettua jakamalla polynomin jokaisen termin yhteisellä tekijällä.
Esimerkki
Erota yhteinen tekijä.
a) \(2x^3+4x^2-2x+8\)
b) \(3x^4+x^2+2x\)
c) \(-6x^3+12x^2-3x\)
d) \(2x^2+5x-3\)
Ratkaisu
a) Jokaisen termin kerroin on jaollinen luvulla 2. Tällöin kertolaskuna kirjoitettu polynomi on
\(2(\frac{2x^3}{2}+\frac{4x^2}{2}-\frac{2x}{2}+\frac{8}{2})\), joka sievenee muotoon \(2(2x^3+2x^2-x+4)\).
b) Jokaisessa termissä on kirjain \(x\). Yhteiseksi tekijäksi valitaan kirjainosista \(x^4\), \(x^2\) ja \(x\) se, jossa on pienin eksponentti, siis tässä tapauksessa \(x\). Kertolaskuna polynomi on siis
\(x(\frac{3x^4}{x}+\frac{x^2}{x}+\frac{2x}{x})\) eli \(x(3x^3+x+2)\).
c) Polynomin kaikki kertoimet ovat jaollisia luvulla 3. Lisäksi jokaisessa termissä esiintyy kirjain \(x\) siten, että termi, jonka eksponentti on pienin, on \(x\). Valitaan yhteiseksi tekijäksi tulo \(3x\). Tällöin polynomi on kertolaskuna
\(3x(-\frac{6x^3}{3x}+\frac{12x^2}{3x}-\frac{3x}{3x})=3x(2x^2+4x-1)\).
d) Ei ole lukua, jolla kaikki polynomin kertoimet voitaisiin jakaa. Kirjainta \(x\) ei esiinny kaikissa polynomin termeissä. Tätä polynomia ei voi muuttaa kertolaskumuotoon tässä luvussa esitetyllä menetelmällä.
