Suorakulmainen koordinaatisto

Eräs suorakulmaisten kolmioiden sovellus on kaksiulotteinen suorakulmainen koordinaatisto. Se koostuu kahdesta lukusuorasta: ”x-akseli” ja ”y-akseli”. Lukusuoran kasvavaa suuntaa merkitään nuolella. Pisteen paikka \(A\) ilmoitetaan muodossa \(A=(x,y)\). Pisteellä \((0,0)\) on erityisnimitys origo.

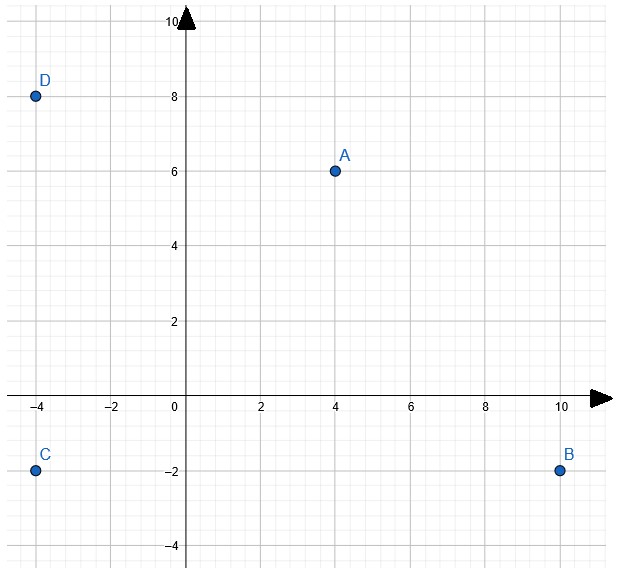
Esim. Kuvassa \(A=(4,6)\), \(B=(10,-2)\), \(C=(-4,-2)\) ja \(D=(-4,8)\).   Pisteiden etäisyys origosta saadaan Pythagoraan lauseella, kun täydennetään kuvio suorakulmaiseksi kolmioksi. Pythagoraan lauseeseen voi sijoittaa myös negatiivisia koordinaattien arvoja.

Esimerkki

Mitkä ovat edellisen kuvan pisteiden \(A\) ja \(D\) etäisyydet origosta?

Ratkaisu

Pisteen \(A\) etäisyys saadaan ratkaisemalla yhtälö:

\(r^2=4^2+6^2\)

\(r=\sqrt{4^2+6^2}\)

\(r\approx 7.2\)

Pisteen \(D\) etäisyys on vastaavasti \(\sqrt{(-4)^2+8^2} = \sqrt{16+64} = \sqrt{80} \approx 8.94\).

Kahden pisteen välisen etäisyyden laskemiseksi tarvitaan pisteiden \(x\)-koordinaattien erotus \(\Delta x\) ja \(y\)-koordinaattien erotus \(\Delta y\). Sen jälkeen sovelletaan näille etäisyyksille Pythagoraan lausetta. Koordinaattien erotukset saadaan vähentämällä ensimmäisen pisteen koordinaatit jälkimmäisistä. Erotuksen voi myös päätellä: kuinka monta askelta x-suunnassa täytyy siirtyä, jotta päästään ensimmäisen pisteet x-koordinaatista jälkimmäisen pisteen x-koordinaattiin? Entä kuinka monta askelta tarvitaan y-suunnassa?

Esimerkki

Laske pisteiden \(A=(4,6)\) ja \(D=(-4,8)\) etäisyys.

Ratkaisu

Aluksi lasketaan x-koordinaattien ero: \(\Delta x = -4-4=-8\), ja y-koordinaattien ero: \(\Delta y = 8-6=2\). Sama tulos saadaan päättelemällä: pisteestä \((4,6)\) pitää siirtyä vaakasuunnassa 8 yksikköä taaksepäin ja 2 yksikköä ylöspäin, jotta päästään pisteeseen \((-4,8)\). Pisteiden välinen etäisyys on siis \(\sqrt{(-8)^2+2^2}=\sqrt{68}\approx 8.24\).

Pisteiden välinen suuntakulma saadaan täydentämällä koordinaatistoon suorakulmainen kolmio ja hyödyntämällä trigonometrisiä funktioita. Matematiikassa käytäntö on, että suuntakulma mitataan positiivisesta x-akselista vastapäivään. Esimerkiksi suunnistuksessa kulma voidaan määritellä eri tavalla.

Esimerkki

Pisteestä \(A=(10,0)\) liikutaan pisteeseen \(B=(25,8)\). Miten pitkä matka siirryttiin ja mihin suuntaan?

Ratkaisu

Siirtymän suuruus on \(\sqrt{(25-10)^2+(8-0)^2} = \sqrt{15^2+8^2} = \sqrt{289} = 17\).

Suuntakulmalle \(\alpha\) pätee \(\tan{\alpha}=\frac{\Delta y}{\Delta x}\), josta saadaan ratkaistua \(\alpha=\arctan{\frac{8-0}{25-10}}=\arctan{\frac{8}{15}} \approx 28.1^{\circ}\).

Esimerkki

Pisteestä \(A=(2,8)\) liikutaan 50 yksikköä 10 asteen suuntakulmassa. Mihin pisteeseen \(B\) päädytään?

Ratkaisu

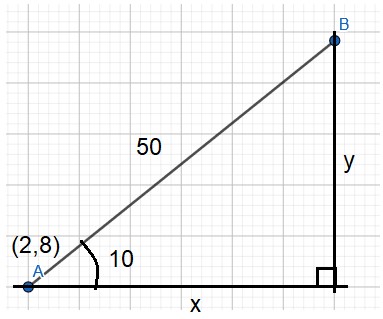
Kuvaan täydennetylle suorakulmaiselle kolmiolle pätee: \(\cos{⁡10^{\circ}}=\frac{\Delta x}{50}\), \(\sin{⁡10^{\circ}}=\frac{\Delta y}{50}\). Siis \(\Delta x=50\cdot \cos{⁡10^{\circ}}=49.2^{\circ}\) ja \(\Delta y=50\cdot \sin{⁡10^{\circ}}=8.7^{\circ}\).

Pisteen \(B\) koordinaatit saadaan lisäämällä x- ja y-suuntainen siirtymä pisteen \(A\) koordinaatteihin: \(B=(2+49.2, 8+8.7)=(51.2,16.7)\).