Kahden vektorin pistetulo

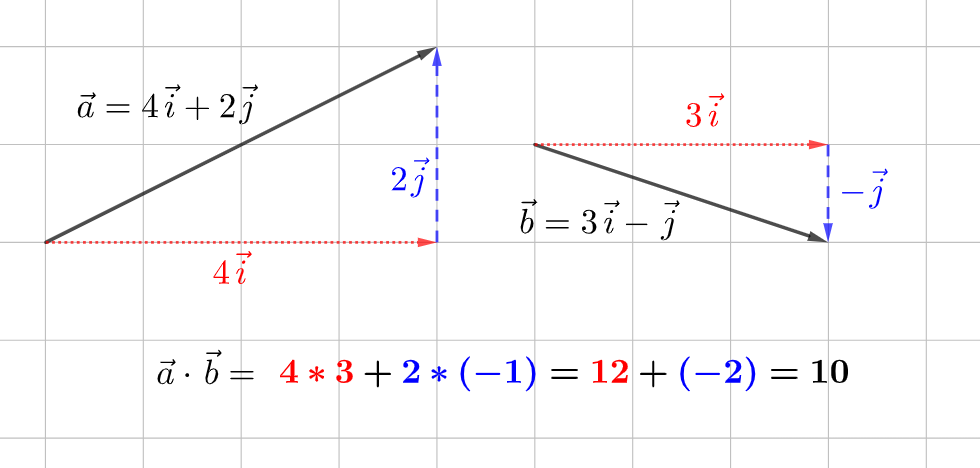
Pistetulon avulla voidaan selvittää vektorien välisiä kulmia, ja sitä tarvitaan myös myöhemmin matriisien laskutoimituksissa. Vektorien \(\vec{a}\) ja \(\vec{b}\) pistetulossa \(\vec{a}\cdot\vec{b}\) vektorien samojen komponenttien kertoimet kerrotaan keskenään, ja tulot lasketaan yhteen. Kuvassa on havainnollistettu vektorien \(\vec{a}=4\vec{i}+2\vec{j}\) ja \(\vec{b}=3\vec{i}-\vec{j}\) pistetuloa \(4\cdot 3 + 2 \cdot (-1)=12-2=10\).

Laskukaava pistetulolle on seuraava: Jos \(\vec{a}=a_x \vec{i}+a_y \vec{j}+a_z \vec{k}\) ja \(\vec{b}=b_x \vec{i}+b_y \vec{j}+b_z \vec{k}\), niin \(\vec{a}\cdot\vec{b}=a_x b_x+a_y b_y+a_z b_z\).

Pistetulon tuloksena on aina luku, ei vektori. Pistetulon toinen nimi, skalaaritulo, korostaakin juuri sitä että tulos on skalaariarvoinen eli luku. Pistetulo merkitään laskuihin pisteellä \(\cdot\) sillä rasti \(\times\) on varattu toiseen laskutoimitukseen.

Pistetulon voi laskea WolframAlphalla merkitsemällä vektorien komponenttien kertoimet sulkuihin tai hakasulkuihin ja kirjoittamalla vektorien väliin pisteen. Edellisen esimerkin pistetulosta saataisiin komennolla [4,2].[3,-1] tulos 10.

Pistetulo ja kohtisuoruus

Jos vektorien pistetulo on nolla, vektorit ovat toisiaan vastaan kohtisuorassa. Perustelu tähän saadaan hieman myöhemmin pistetulon geometrisen määritelmän avulla. Sääntö toimii myös kolmiulotteisen koordinaatiston vektoreille.

Esimerkki

Laske kuvan vektorien väliset pistetulot. Ovatko annetut vektorit kohtisuorassa toisiaan vastaan?

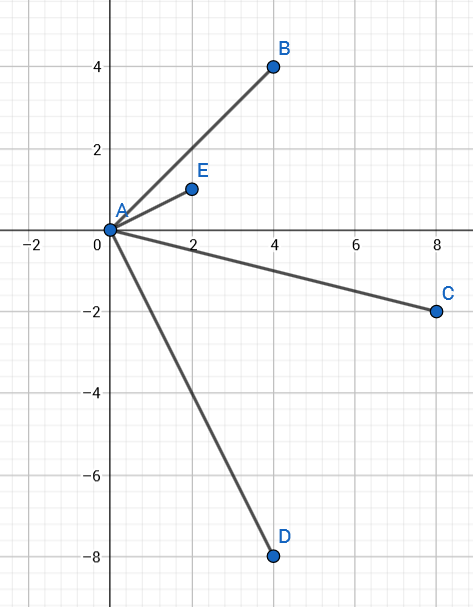
a) \(\vec{AB}=4\vec{i}+4\vec{j}\) ja \(\vec{AC}=8\vec{i}-2\vec{j}\)

b) \(\vec{AD}=4\vec{i}-8\vec{j}\) ja \(\vec{AE}=2\vec{i}+\vec{j}\)

Ratkaisu

a) Pistetulo on \(4\cdot 8+4\cdot (-2)=32-8=24\). Vektorit eivät ole toisiaan vastaan kohtisuorassa.

b) Pistetulo on \(4\cdot 2-8\cdot 1=0\). Vektorit ovat toisiaan vastaan kohtisuorassa.

Esimerkki

Laske vektorien \(\vec{a}\) ja \(\vec{b}\) pistetulo. Ovatko vektorit kohtisuorassa toisiaan vastaan?

a) \(\vec{a}=2\vec{i}+6\vec{j}, \vec{b}=-3\vec{i}-\vec{j}\)

b) \(\vec{a}=7\vec{i}-\vec{j}, \vec{b}=2\vec{j}+\vec{k}\)

c) \(\vec{a}=2\vec{i}-3\vec{j}+\vec{k}, \vec{b}=4\vec{i}+\vec{j}-\vec{k}\)

Ratkaisu

a) \(\vec{a}\cdot \vec{b}=2\cdot (-3)+6\cdot (-1)=-6-6=-12 \neq 0\), joten eivät ole kohtisuorassa.

b) \(\vec{a}\cdot \vec{b}=7\cdot 0+(-1)\cdot 2+0\cdot 1=-2 \neq 0\), joten eivät ole kohtisuorassa.

c) \(\vec{a}\cdot \vec{b}=2\cdot 4+(-3)\cdot 1+1\cdot (-1)=0\), joten \(\vec{a} \perp \vec{b}\).

Esimerkki

Mikä tulee luvun \(s\) olla, jotta vektorit \(\vec{a}\) ja \(\vec{b}\) olisivat kohtisuorassa toisiaan vastaan?

a) \(\vec{a}=100 \vec{i}+75\vec{j}\) ja \(\vec{b}=s\vec{i}-2\vec{j}\)

b) \(\vec{a}=\vec{i}+2\vec{j}+\vec{k}\) ja \(\vec{b}=s\vec{i}+\vec{j}-\vec{k}\)

Ratkaisu

a) Pistetulo on \(\vec{a}\cdot \vec{b}=100\cdot s+75\cdot (-2)=100s-150\). Koska toisiaan vastaan kohtisuorien vektorien pistetulo on nolla, niin ratkaistaan yhtälö \(100s-150=0\). Tästä saadaan helposti \(s=1.5\).

b) Pistetulo on \(\vec{a}\cdot \vec{b}=1\cdot s+2\cdot 1+1\cdot (-1)=s+1\), joten tulee olla \(s+1=0\) eli \(s=-1\).

Vektorien välinen kulma

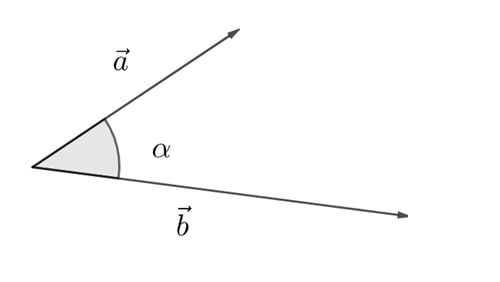
Vektorien pistetulolle on olemassa myös ns. geometrinen määritelmä \(\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}| \cos{\alpha}\), missä \(\alpha\) on vektorien \(\vec{a}\) ja \(\vec{b}\) välinen kulma. Kaavan voi perustella kosinilauseen avulla.

Kaavan perustelu

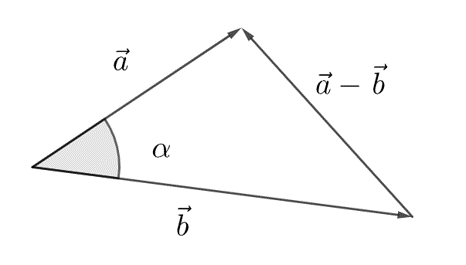
Kuvan kolmiossa kulman \(\alpha\) kyljet ovat vektorit \(\vec{a}\) ja \(\vec{b}\). Kulmaa vastapäätä oleva sivu saadaan esitettyä näillä vektoreilla muodossa \(\vec{a}-\vec{b}\). Kolmion sivujen pituudet ovat näiden vektorien avulla ilmaistuna \(|\vec{a}|\), \(|\vec{b}|\) ja \(|\vec{a}-\vec{b}|\). Kirjoitetaan näitä merkintöjä käyttäen kosinilause:

\(|\vec{a}-\vec{b}|^2 =|\vec{a}|^2 + |\vec{b}|^2 - 2 |\vec{a}| |\vec{b}| \text{cos}~\alpha\)

Seuraavaksi johdetaan toinen esitysmuoto yhtälön vasemmalle puolelle \(|\vec{a}-\vec{b}|^2\). Esitetään vektorit kantavektorien avulla, siis \(\vec{a}=a_x \vec{i} + a_y \vec{j} + a_z \vec{k}\) ja \(\vec{b}=b_x \vec{i} + b_y \vec{j} + b_z \vec{k}\).

Vektorien erotus on tällöin \(\vec{a}-\vec{b}=(a_x-b_x) \vec{i} + (a_y-b_y) \vec{j} + (a_z-b_z) \vec{k}\). Tämän vektorin pituuden toinen potenssi on \(|\vec{a}-\vec{b}| = (a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2\). Oikea puoli voidaan potenssilukujen laskusääntöjen mukaisesti sieventää seuraavasti:

\((a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 = \dots \)

\( = a_x^2-2 a_x b_x + b_x^2 + a_y^2-2 a_y b_y + b_y^2 + a_z^2 + 2 a_z b_z + b_z^2\)

Järjestellään oikean puolen termejä:

\((a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 = \dots \)

\( = a_x^2+a_y^2+a_z^2 + b_x^2 + b_y ^2 + b_z^2 - 2a_x b_x -2 a_y b_y -2 a_z b_z\)

Huomataan, että oikealta puolelta löytyy vektorien pituuksien neliöt:

\((a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2a_x b_x -2 a_y b_y -2 a_z b_z\)

Yhtälön oikean puolen viimeiset termit voidaan ryhmitellä seuraavasti:

\((a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2(a_x b_x+ a_y b_y + a_z b_z)\)

eli pistetulon määritelmän mukaan

\((a_x-b_x)^2 + (a_y-b_y)^2 + (a_z-b_z)^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2 \vec{a} \cdot \vec{b}\)

Saatiin siis tulos:

\(|\vec{a}-\vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2 \vec{a} \cdot \vec{b}\)

Näin ollen kosinilauseen voi kirjoittaa muodossa:

\(|\vec{a}|^2 + |\vec{b}|^2 - 2 \vec{a} \cdot \vec{b} = |\vec{a}|^2 + |\vec{b}|^2 - 2 |\vec{a}| |\vec{b}| \text{cos}~\alpha\)

Tämä sievenee muotoon

\( \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \text{cos}~\alpha\)

Edellisestä kaavasta saadaan ratkaistua \(\text{cos}~\alpha=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\). Kulma \((\alpha\) saadaan edellisen laskun tuloksesta arkuskosinin avulla: \(\alpha=\text{acos}~\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\).

Laskun tuloksen voi tarkistaa WolframAlphan komennolla angle between. Esimerkiksi vektorien \(3\vec{i}+2\vec{j}-4\vec{k}\) ja \(\vec{i}-\vec{j}+5\vec{k}\) välisen kulman saa komennolla angle between ([3,2,-4],[1,-1,5]).

Esimerkki

Laske vektorien \(\vec{a}\) ja \(\vec{b}\) välinen kulma, kun vektorit ovat seuraavat:

a) \(\vec{a}=31 \vec{i}-26\vec{j},\vec{b}=91\vec{i}+42\vec{j}\),

b) \(\vec{a}=3\vec{i}-\vec{j}+7\vec{k}, \vec{b}=-3\vec{i}+4\vec{j}+2\vec{k}\).

Ratkaisu

a) \(\cos{\alpha} = \frac{31\cdot 91-26\cdot 42}{\sqrt{31^2+91^2}\sqrt{(-26)^2+42^2}} \approx 0.426\), joten \(\alpha=\arccos{⁡0.426} \approx 64.8^{\circ}\).

Ratkaisu WolframAlphalla: angle between [31,-26],[91,42] tai (31*91-26*42)/(sqrt(31^2+26^2)*sqrt(91^2+42^2))

b) \(\cos{\alpha} = \frac{(3\cdot (-3)-1\cdot 4+7\cdot 2}{\sqrt{3^2+(-1)^2+7^2}\sqrt{(-3)^2+4^2+2^2}}\approx 0.0242\), joten \(\alpha =\arccos{⁡0.0242} \approx 88.6^{\circ}\).

Ratkaisu WolframAlphalla: angle between [3,-1,7],[-3,4,2] tai (3*(-3)-1*4+7*\2)/(sqrt(3^2+1^2+7^2)*sqrt((-3)^2+4^2+2^2))

Esimerkki

a) Vektorin \(\vec{a}\) pituus on 65 ja vektorin \(\vec{b}\) pituus on 20. Vektorien välinen kulma on 30 astetta. Mikä on vektorien \(\vec{a}\) ja \(\vec{b}\) pistetulo?

b) Vektorin \(\vec{a}\) pituus on 12 ja vektorin \(\vec{b}\) pituus on 4. Vektorien \(\vec{a}\) ja \(\vec{b}\) pistetulo on 16. Mikä on vektorien \(\vec{a}\) ja \(\vec{b}\) välinen kulma?

Ratkaisu

a) \(\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}| \cos{\alpha} = 65\cdot 20 \cdot \cos{30^{\circ}} \approx 1125.83\)

b) Pistetulon geometrisesta määritelmästä saadaan ratkaistua: \(\cos{\alpha} = \frac{\vec{a}\cdot \vec{b}}{|\vec{a}||\vec{b}|}\), joten tässä tapauksessa kulman kosini on \(\cos{\alpha} = \frac{16}{2\cdot 4}=\frac{16}{48}=\frac{1}{3}\). Kulmaksi saadaan \(\alpha = \arccos{\frac{1}{3}} \approx 70.53^{\circ}\).

Esimerkki

Tie haarautuu pisteessä (150,200) kahdeksi suoraksi tieksi siten, että toinen haara päätyy pisteeseen (220,350) ja toinen pisteeseen (240,100).

a) Muodosta kaksi vektoria, jotka kuvaavat risteyksestä lähteviä teitä.

b) Laske pistetulon avulla teiden välinen kulma.

Ratkaisu

Vektorit ovat \((220-150) \vec{i}+(350-200) \vec{j}=70 \vec{i}+150 \vec{j}\) ja \((240-150) \vec{i} +(100-200) \vec{j}=90 \vec{i}-100\vec{j}\).

Kulman kosini on \(\cos{\alpha}=\frac{70\cdot 90+150\cdot (-100}{\sqrt{70^2+150^2}\sqrt{90^2+(-100)^2}} \approx -0.391\), joten kulmaksi saadaan \(\alpha = \arccos{-0.391} = 113^{\circ}\).

Pistetulon merkitys

Laskemalla pistetulo saadaan jokin luku. Mitä luvusta oikein voi päätellä? Pistetulon \(\vec{a}\cdot\vec{b}\) arvo riippuu kahdesta asiasta:

• vektorien \(\vec{a}\) ja \(\vec{b}\) pituuksista

• vektorien \(\vec{a}\) ja \(\vec{b}\) suunnista toisiinsa nähden

Pistetulon merkki kertoo vektorien suunnista toisiinsa nähden seuraavan kuvan mukaisesti. Pelkästään sen perusteella, onko pistetulo positiivinen vai negatiivinen, voidaan päätellä, osoittavatko vektorit suunnilleen samaan suuntaan, vai eri suuntiin. Merkki kertoo suunnista seuraavasti:

• jos \(\vec{a}\cdot\vec{b} > 0\), niin vektorien \(\vec{a}\) ja \(\vec{b}\) välinen kulma on terävä

• jos \(\vec{a}\cdot\vec{b} = 0\), niin vektorit \(\vec{a}\) ja \(\vec{b}\) ovat kohtisuorassa toisiaan vastaan

• jos \(\vec{a}\cdot\vec{b} < 0\), niin vektorien \(\vec{a}\) ja \(\vec{b}\) välinen kulma on tylppä

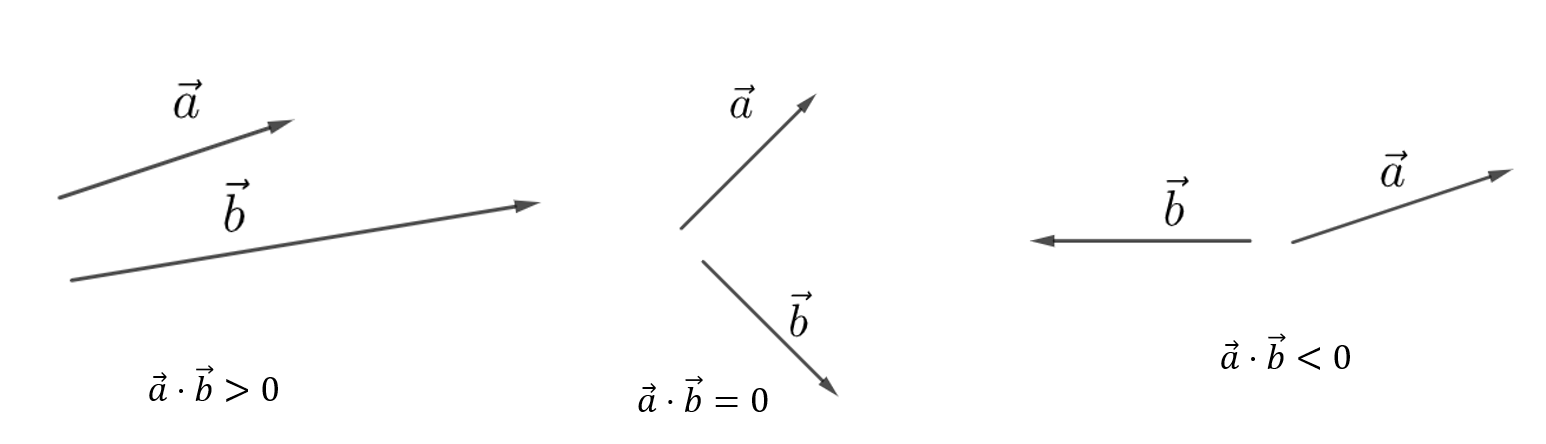
Eräs tapa hahmottaa pistetulon merkitystä on seuraavassa kuvassa esitetty vertaus sateella ämpäriin kertyvästä vedestä. Ajatellaan, että vesisade vastaa vektoria \(\vec{a}\) ja ämpäri vektoria \(\vec{b}\). Vektorin \(\vec{a}\) pituus kuvaa vesisateen voimakkuutta ja vektorin \(\vec{b}\) pituus ämpärin suuruutta. Ajatellaan tässä vektorien suunnat niin, että vesisade ja ämpäri osoittavat samaan suuntaan silloin, kun ämpärin aukko on kohti taivasta. Eniten vettä kertyy ämpäriin, kun ämpäri on pystyssä, ja hieman vähemmän silloin, kun ämpäri on vinossa. Jos ämpäri on kyljellään, vettä ei kerry sinne lisää, mutta ei valu poiskaan. Jos ämpärin suu osoittaa alaviistoon tai suoraan alaspäin, vettä valuu ämpäristä pois.