Vektorit ja tasot

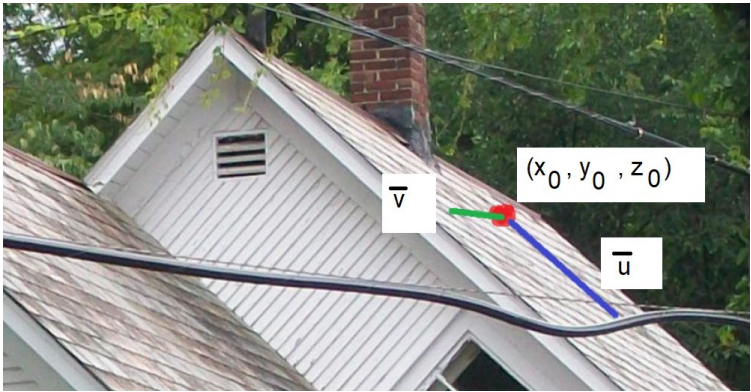
Tasokin voidaan esittää vektorien avulla. Tason määrää jokin tasolla oleva piste \((x_0,y_0,z_0)\) sekä kaksi tason suuntaista, mutta keskenään erisuuntaista vektoria \(\vec{u}=u_x \vec{i} + u_y \vec{j} + u_z \vec{k}\) ja \(\vec{v}=v_x \vec{i} + v_y \vec{j} + v_z \vec{k}\). Piste pitää nyt ilmaista kolmella koordinaatilla, sillä pistehän ei välttämättä ole “lattian tasossa”. Myös tason vektoreissa pitää olla kolme komponenttia, sillä taso voi hyvinkin olla vinossa, kuten kuvassa esitetty katto.

Logiikka on siis sama kuin vektorien avulla esitetyissä suorissa: ensin valitaan jokin piste, joka varmasti on tasolla, ja sitten määritellään, mihin suuntaan liikkumalla tasolla pysytään. Nyt suuntia kuitenkin tarvitaan kaksi, tai muuten käveltäiisiin pelkästään viivaa pitkin tasolla. Kuvan tapauksessa vektorit ovat räystään ja katonharjan suuntaiset, mutta suunnat voisivat olla jotkin muutkin. Lisäksi on hyvä tietää, että yleisesti ottaen tasot oletetaan äärettömyyksiin asti jatkuviksi, toisin kuin katot. Katolla ei pysy, vaikka liikkuisi säntillisesti katon määrittävien vektorien suunnassa, jos liikkuu liian pitkälle.

Tason vektorit voidaan muodostaa, jos tunnetaan jotkin tasolla olevat pisteet \(A\), \(B\) ja \(C\). Tällöin vektoreiksi voidaan valita esimerkiksi \(\vec{AB}\) ja \(\vec{AC}\). Tasolla olevan pisteen \((x_0,y_0,z_0)\) paikkavektori on \(\vec{r_0}=x_0 \vec{i} + y_0 \vec{j} + z_0 \vec{k}\). Näistä vektoreista voidaan muodostaa vektorimuotoinen parametriesitys \(\vec{r}\) samalla tavalla kuin suorien tapauksessa:

\(\vec{r}=\vec{r_0}+s\vec{u}+t\vec{v}, s, r \in \Re\).

Erona suoraan on vain se, että vapaasti valittavia kertoimia on nyt kaksi, siis \(s\) ja \(t\). Vektorimuotoisesta parametriesityksestä voidaan muodostaa myös koordinaattimuotoinen parametriesitys:

\(\begin{equation}\begin{cases}x=x_0+s u_x + t v_x \\ y=y_0 + s u_y + t v_y \\ z=z_0 + s u_z + t v_z \end{cases}\end{equation}\)

Esimerkki

Eräällä tasolla ovat pisteet \(A=(2,1,3)\), \(B=(0,2,1)\) ja \(C=(3,2,-4)\). Muodosta tason vektori- ja koordinaattimuotoinen parametriesitys.

Ratkaisu

Muodostetaan tason suuntaiset vektorit:

\(\vec{AB}=(0-2)\vec{i}+(2-1)\vec{j}+(1-3)\vec{k}=-2\vec{i}+\vec{j}-2\vec{k}\),

\(\vec{AC}=(3-2)\vec{i}+(2-1)\vec{j}+(-4-3)\vec{k}=\vec{i}+\vec{j}-7\vec{k}\)

Vektoriksi \(\vec{r_0}\) käy minkä tahansa pisteen \(A\), \(B\) tai \(C\) paikkavektori, esimerkiksi \(\vec{OA}=2\vec{i}+\vec{j}+3\vec{k}\).

Vektorimuotoinen parametriesitys \(\vec{r}=\vec{r_0}+s\vec{u}+t\vec{v}\):

\(\vec{r}=2\vec{i}+\vec{j}+3\vec{k}+s(-2\vec{i}+\vec{j}-2\vec{k})+t(\vec{i}+\vec{j}-7\vec{k})\)

\(\vec{r}=2\vec{i}+\vec{j}+3\vec{k}-2s\vec{i}+s\vec{j}-2s\vec{k})+t\vec{i}+s\vec{j}-7t \vec{k}\)

\(\vec{r}=(2-2s+t)\vec{i}+(1+s+t)\vec{j}+(3-2s-7t)\vec{k}\)

Koordinaattimuotoinen parametriesitys on

\(\begin{equation}\begin{cases}x=2-2s+t \\ y=1+s+t \\ z=3-2s-7t \end{cases}\end{equation}\)

Nyt voitaisiin laskea tasolla olevia pisteitä \((x,y,z)\) valitsemalla jotkin arvot \(s\) ja \(t\). Jos esimerkiksi \(s=3\) ja \(t=1\), niin saadaan eräs tasolla oleva piste \((2-6+1,1+3+1,3-6-7)=(-3,5,-10)\).

Tason yhtälö

Tasollekin voidaan muodostaa yhtälö. Tason yhtälön määrää tason määrittelevien vektorien ristitulo. Kyseessä on tason normaalivektori, eli vektori joka on kohtisuorassa kumpaakin vektoria \(\vec{u}\) ja \(\vec{v}\) vastaan. Jos ristitulosta muodostuva vektori kirjoitetaan \(\vec{n} = n_x \vec{i} + n_y \vec{j} + n_z \vec{k}\), ja tasolta tiedetään mikä tahansa piste \((x_0, y_0, z_0)\), niin tason yhtälö on

\(n_x(x-x_0)+n_y(y-y_0)+n_z (z-z_0)=0\)

Esimerkki

Taso kulkee pisteen \((2,1,3)\) kautta ja on vektorien \(\vec{u}=-2\vec{i}+\vec{j}-2\vec{k}\) ja \(\vec{v}=\vec{i}+\vec{j}-7\vec{k}\) suuntainen. Muodosta tason yhtälö.

Ratkaisu

Ristitulon voi laskea tietokoneella tai käsin ainakin kerrattuaan ristitulon laskusäännöt. Suuntavektorien ristitulo on \(\vec{u} \times \vec{v} = -5\vec{i}-16\vec{j}-3\vec{k}\).

Tason yhtälö on siis \(-5(x-2)-16(y-1)-3 (z-3)=0\).

Avataan sulut: \(-5x+10-16y+16-3z+9=0\)

Yhdistetään vakiot: \(-5x-16y-3z+25=0\)

Suoran ja tason leikkauspiste

Suoraan ja tasoon liittyviä kaavoja voidaan toki yhdistääkin. Erityisesti suoran ja tason leikkauspiste saadaan suoran koordinaattimuotoisen parametriesityksen ja tason koordinaattimuotoisen yhtälön avulla. Käsitellään tässä kolmessa ulottuvuudessa määriteltyä suoraa.

Esimerkki

Oletetaan, että suora on määritelty koordinaattimuotoisella parametriesityksellä:

\(\begin{equation}\begin{cases} x=1+2t, y=-1+t, z=2-t\end{cases}\end{equation}\)

Oletetaan, myös, että tason yhtälö on \(2x+3y+4z-10=0\).

Leikkauspiste löytyy, kun suoran pisteet ovat samalla tason pisteitä. Sijoitetaan siis tason yhtälöön suoran pisteiden määritelmät:

\(2(1+2t)+3(-1+t)+4(2-t)-10=0\)

Sievennetään ja ratkaistaan \(t\):

\(2+4t-3+3t+8-4t-10=0\)

\(3t-3=0\)

\(t=1\)

Suora ja taso siis leikkaavat kun \(t=1\). Tällöin koordinaatit ovat \(x = 1 + 2 \cdot 1 = 3\), \(y = −1 + 1 = 0\), \(z = 2 − 1 = 1\). Leikkauspiste on siis (3,0,1).

Joskus leikkauspisteitä ei löydy ollenkaan ja joskus niitä löytyy äärettömän monta. Yhtään leikkauspistettä ei ole, kun suora ja taso ovat saman suuntaisia mutta eivät päällekkäin, esimerkiksi köydenvedossa kun narua vedetään kahdesta päästä samalla korkeudelta maanpinnasta. Kun köysi lasketaan vetoerien välissä lepäämään maahan, se osuu tasoon äärettömän monessa pisteessä.