Vektorien venyttelyä
Contents
Vektorien venyttelyä#
Vektorien yhteen- ja vähennyslasku tapahtuu komponenteittain, kuten esitettiin vektorien perusteiden yhteydessä. Muita helppoja vektorien laskutoimituksia ovat vektorin pituuden laskeminen ja vektorin kertominen reaaliluvulla. Nämä kaksi laskutoimitusta yhdistämällä voidaan muodostaa eräs erityinen vektori, yksikkövektori. Myöhemmin opetellaan myös muita laskutoimituksia: pistetulo ja ristitulo.
Vektorin pituuden laskeminen#
Vektorin \(\vec{a}\) pituutta merkitään itseisarvomerkeillä, siis \(|\vec{a}|\). Kahta pistettä yhdistävän vektorin pituus on lyhin etäisyys kyseisten pisteiden välillä.
Jos vektorissa \(\vec{a}\) on vain yksi komponentti, niin vektorin pituus on sama kuin komponentin kertoimen itseisarvo. Esimerkiksi vektorin \(3\vec{j}\) pituus on 3 ja vektorin \(-2 \vec{k}\) pituus on \(|-2|=2\).
Yleisesti vektorin \(\vec{a}\) pituuden \(|\vec{a}|\) laskeminen perustuu Pythagoraan lauseeseen. Tarkastellaan aluksi kaksiulotteista tapausta. Kaksiulotteinen vektori \(\vec{a}\) on hypotenuusa suorakulmaisessa kolmiossa, jonka kateetit ovat yksikkövektorit \(\vec{i}\) ja \(\vec{j}\) kertoimineen, siis \(a_x \vec{i}\) ja \( a_y\vec{j}\). Tällöin vektorin pituus saadaan yhtälöstä
\(|\vec{a}|^2 = |a_x \vec{i}|^2 + |a_y \vec{j}|^2\) eli \(|\vec{a}|^2 = |a_x|^2 + |a_y|^2\), josta voidaan ratkaista \(|\vec{a}| = \sqrt{|a_x|^2 + |a_y|^2}\).
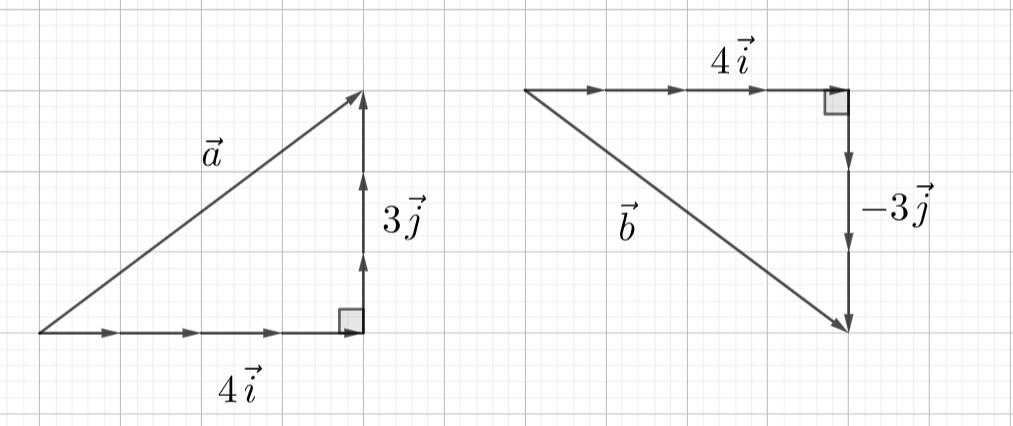
Vektorin suunta ei siis vaikuta vektorin pituuteen. Seuraavan kuvan vektorit \(\vec{a}=4 \vec{i} +3 \vec{j}\) ja \(\vec{b}=4 \vec{i} - 3 \vec{j}\) ovat yhtä pitkiä, vaikka vektorissa \(\vec{b}\) on negatiivinen kerroin. Kummankin pituus on \(\sqrt{4^2+3^2}=5\). Saman pituisia ovat myös vektorit \(-4 \vec{i} + 3 \vec{j}\) ja \(-4 \vec{i} - 3 \vec{j}\).
Kolmessa ulottuvuudessa vektorin pituuden laskukaavaksi voidaan johtaa vastaavasti \(|\vec{a}| = \sqrt{a_x^2 + a_y^2 + a_z^2}\). Tässä huomioitavaa on, että vaikka komponentteja on kolme, eksponenttina potenssiinkorotuksissa on edelleen luku 2, ja lopuksi pitää laskea neliöjuuri eikä kuutiojuurta.
WolframAlphalla vektorin pituuden saa komennolla norm, jonka perään tulee sulut ja niiden sisään hakasuluissa vektorien komponentit. Esimerkiksi vektorin \(3\vec{i}-8\vec{j}+4\vec{k}\) pituuden saa kirjoittamalla norm([3,-8,4]).
Esimerkki
Laske vektorien pituus.
a) \(8 \vec{i} + 6 \vec{j}\)
b) \(-4 \vec{i} + 3 \vec{j}\)
c) \(2 \vec{i} + 6 \vec{j} - 3 \vec{k}\)
Ratkaisu
a) \(|8\vec{i}+6\vec{j}|=\sqrt{8^2+6^2}=\sqrt{100}=10\)
b) \(|-4 \vec{i}+3\vec{j}|=\sqrt{(-4)^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\)
c) \(|2 \vec{i}+6\vec{j}-3\vec{k}|=\sqrt{2^2+6^2+(-3)^2}=\sqrt{49}=7\)
Esimerkki
a) Määritä luvulle \(t\) sellainen arvo, että vektorin \(\vec{a}=-2\vec{i}+t\vec{j}\) pituus on 5.
b) Määritä luvulle \(s\) sellainen arvo, että vektorin \(\vec{b}=s\vec{i}+3s\vec{j}\) pituus on 130.
Ratkaisu
a) Vektorin pituus on \(|\vec{a}|=\sqrt{(-2)^2+t^2}=\sqrt{4+t^2}\).
Ratkaistaan yhtälö:
\(\sqrt{4+t^2}=5\)
\(4+t^2=25\)
\(t^2 = 21\)
\(t= \pm \sqrt{21}\)
b) Vektorin pituus on \(|\vec{b}|=\sqrt{s^2+(3s)^2}=\sqrt{s^2+9s^2}=\sqrt{10s^2}\).
Ratkaistaan yhtälö:
\(\sqrt{10s^2} = 130\)
\(10s^2 = 130^2\)
\(s^2=\frac{130^2}{10}\)
\(s=\pm \sqrt{\frac{130^2}{10}}\)
Vektorin kertominen luvulla#
Vektori \(\vec{a}\) voidaan kertoa reaaliluvulla \(p\) siten, että jokaisen komponentin kerroin kerrotaan kyseisellä luvulla.
Jos \(\vec{a}=a_x \vec{i}+a_y \vec{j}+a_x \vec{k}\), niin \(p\vec{a}=pa_x \vec{i}+pa_y \vec{j}+pa_z \vec{k}\).
WolframAlphalla kertominen tapahtuu tähtimerkillä *. Esimerkiksi lasku \(2\vec{a}\), missä \(\vec{a}=3\vec{i}-8\vec{j}+4\vec{k}\), onnistuu komennolla 2*[3,-8,4].
Vektorin voi jakaakin luvulla. Tällöin vektorin jokaisen komponentin kerroin jaetaan kyseisellä luvulla. Laskua merkitään kuitenkin yleensä siten, että vektori kerrotaan tämän luvun käänteisluvulla.
Esimerkiksi vektori \(8 \vec{i}-12 \vec{j}\) jaetaan luvulla 4 suorittamalla laskutoimitus
\(\frac{1}{4}(8 \vec{i} - 12 \vec{j}) = \frac{8}{4} \vec{i} -\frac{12}{4} \vec{j} = 2 \vec{i} -3 \vec{j}\).
Luvulla kerrottaessa vektorin suunta ja pituus voi muuttua:
jos \(0 < p < 1\), vektorin suunta säilyy samana, mutta vektori lyhenee
jos \( p > 1\), vektorin suunta säilyy samana, mutta vektorin pituus kasvaa
jos \(-1 < p < 0\), vektori kääntyy toisin päin ja lyhenee
jos \(p < -1\), vektori kääntyy toisin päin ja sen pituus kasvaa
Esimerkki
Olkoon eräs vektori \(\vec{a}=\frac{1}{2} \vec{i}+3 \vec{j}\). Mitä on
a) \(3\vec{a}\), b) \(-2\vec{a}\) ?
Ratkaisu
a) \(3 \vec{a} =3\left(\frac{1}{2} \vec{i} + 3 \vec{j} \right)= 3 \cdot \frac{1}{2} \vec{i} + 3\cdot 3 \vec{j} = 1.5 \vec{i}+9\vec{j}\)
b) \(-2 \vec{a}=-2\left(\frac{1}{2} \vec{i}+3 \vec{j}\right)=-2\cdot \frac{1}{2} \vec{i}+(-2)\cdot 3 \vec{j}=-\vec{i}-6\vec{j}\)
Esimerkki
Olkoot vektorit \(\vec{A}=2\vec{i}+8\vec{j}\) ja \(\vec{B}=-3 \vec{i}+\vec{j}\). Tee seuraavat laskutoimitukset:
a) \(\vec{A}+\vec{B}\), b) \(2\vec{A}-\vec{B}\), c) \(|3\vec{A}|\), d) \(|\vec{A}-\vec{B}|\)
Ratkaisu
a) \(\vec{A}+\vec{B}=(2+(-3)) \vec{i} +(8+1) \vec{j}=-\vec{i}+9\vec{j}\)
b) \(2\vec{A}-\vec{B}=(2\cdot 2 \vec{i} +2 \cdot 8 \vec{j})-(-3 \vec{i} + \vec{j})=4 \vec{i}+16 \vec{j} +3 \vec{i}-\vec{j}=7 \vec{i}+15\vec{j}\)
c) \(|3\vec{A}|=|3 \cdot 2 \vec{i}+3 \cdot 8 \vec{j}|=|6 \vec{i}+24\vec{j}|=\sqrt{6^2+24^2}=\sqrt{612}\approx 24.7\)
d) \(|\vec{A}-\vec{B}|=|(2-(-3)) \vec{i}+(8-1) \vec{j}|=|5 \vec{i} +7 \vec{j}|=\sqrt{5^2+7^2}=\sqrt{74} \approx 8.6\)
Huom! Vektorien erotuksen pituus ei ole sama kuin vektorien pituuksien erotus!
Esimerkki
Millä luvulla \(p\) vektori \(\vec{a}=3 \vec{i}+5 \vec{j}\) pitää kertoa, jotta vektorin \(p\vec{a}\) pituus olisi 30?
Ratkaisu
Kirjoitetaan vektorin \(p\vec{a}\) eli \(3p\vec{i}+5p\vec{j}\) pituus:
\(|p\vec{a}|=|3p\vec{i}+5p\vec{j}|=\sqrt{(3p)^2+(5p)^2}=\sqrt{(9p^2+25p^2}=\sqrt{34p^2}\)
Ratkaistaan yhtälö:
\(\sqrt{34p^2}=30\)
\(34 p^2 = 30^2\)
\(p^2 = \frac{30^2}{34}\)
\(p = \pm \sqrt{\frac{30^2}{34}}\)
\(p = \pm \frac{\sqrt{30^2}}{\sqrt{34}}\)
\(p = \pm \frac{30}{\sqrt{34}}\)
\(p \approx \pm 5.14\)
Vektorien yhdensuuntaisuus#
Vektorit \(\vec{a}\) ja \(\vec{b}\) ovat yhdensuuntaiset, jos vektori \(\vec{b}\) saadaan kertomalla vektori \(\vec{a}\) jollakin luvulla \(p\), siis \(\vec{b}=p\vec{a}\).
Yhdensuuntaiset vektorit ovat samansuuntaiset, jos \(p > 0\). Tällöin ne osoittavat samaan suuntaan, mutta voivat olla eri pituiset.
Yhdensuuntaiset vektorit ovat vastakkaissuuntaiset, jos \(p < 0\). Tällöin vektorit osoittavat vastakkaisiin suuntiin ja voivat olla eri pituiset.
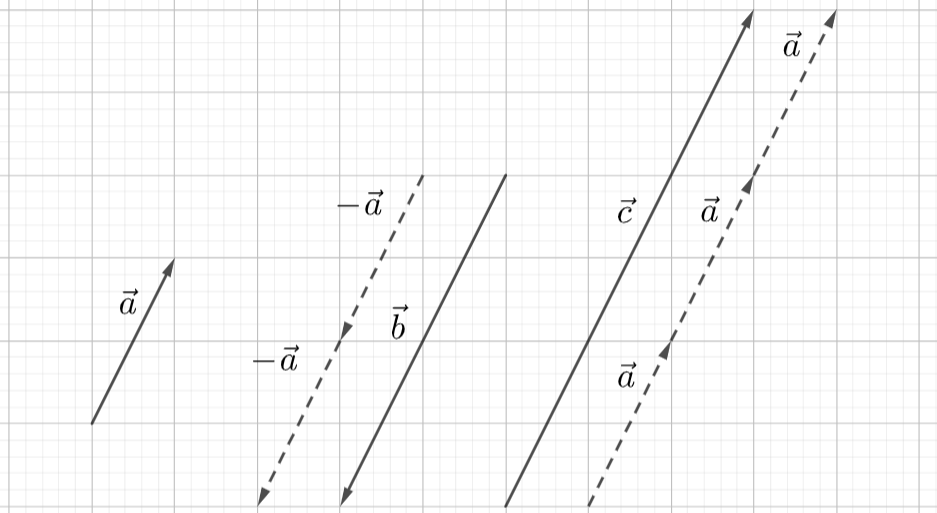
Kuvassa vektorit \(\vec{a}\) ja \(\vec{c}\) ovat samansuuntaiset, sillä \(\vec{c}=3\vec{a}\). Vektorit \(\vec{a}\) ja \(\vec{b}\) ovat vastakkaissuuntaiset, sillä \(\vec{b}=-2\vec{a}\). Kaikki kuvan vektorit \(\vec{a}, \vec{b}\) ja \(\vec{c}\) ovat keskenään yhdensuuntaisia.
Esimerkki
Millä luvun \(a_x\) arvolla vektorit \(\vec{a}=a_x \vec{i} + 2 \vec{j}\) ja \(\vec{b}=3 \vec{i} + 8 \vec{j}\) ovat samansuuntaiset?
Ratkaisu
Kun vektori \(\vec{a}\) kerrotaan luvulla \(p\), tuloksena on \(p\vec{a}=pa_x \vec{i} + 2p \vec{j}\). Tämän tulee olla sama kuin \(3\vec{i} + 8 \vec{j}\). Yhtäsuuruus pätee vektorien komponenteille yksitellen: tulee olla \(pa_x = 3\) ja \(2p=8\). Jälkimmäisestä ehdosta voidaan ratkaista, että \(p=4\). Nyt voidaan ratkaista \(a_x\) yhtälöstä \(4a_x=3\), siis \(a_x=\frac{3}{4}\).
Huomaa, että saatu vastaus ei ole ainoa mahdollinen ratkaisu. Esimerkiksi vektori \(\frac{3}{2} \vec{i} + 4\vec{j}\) on myös samansuuntainen vektorin \(\vec{b}\) kanssa, sillä vektori \(\vec{b}\) saadaan kertomalla kyseinen vektori luvulla 2. Oleellista on, että vektorissa \(\vec{a}\) komponenttien kertoimien suhde on sama kuin ratkaisuksi saadussa vektorissa.
Yksikkövektori#
Vektorin \(\vec{a}\) suuntainen yksikkövektori \(\vec{a}^0\) määritellään \(\vec{a}^0=\frac{\vec{a}}{|\vec{a}|}\). Yksikkövektorin pituus on nimensä mukaisesti 1. Yksikkövektoreita tarvitaan myöhemmin mm. vektoriprojektioiden laskemisessa. Yksikkövektori voidaan laskea sekä kaksi- että kolmiulotteisen koordinaatiston vektoreille. Yksikkövektorille käytetään myös merkintätapaa \(\hat{\mathbf{a}}\).
Esimerkki
Määritä vektorin \(2\vec{i}-\vec{j}\) suuntainen yksikkövektori.
Ratkaisu
Vektori on \(\frac{2 \vec{i}-\vec{j}}{|2\vec{i}-\vec{j}|}=\frac{2\vec{i}-\vec{j}}{\sqrt{2^2+(-1)^2}}=\frac{2\vec{i}-\vec{j}}{\sqrt{5}}=\frac{2}{\sqrt{5}} \vec{i}-\frac{1}{\sqrt{5}} \vec{j}\).
Esimerkki
Määritä yksikkövektori, joka on pisteiden \((20,6,2)\) ja \((3,1,10)\) välisen vektorin suuntainen.
Ratkaisu
Pisteiden välinen vektori on
\((3-20)\vec{i}+(1-6)\vec{j}+(10-2)\vec{k}=-17\vec{i}-5\vec{j}-8\vec{k}\),
ja vektorin pituus on \(\sqrt{(-17)^2+(-5)^2+(-8)^2}=\sqrt{378}\).
Yksikkövektori on siis
\(\frac{-17}{\sqrt{378}} \vec{i}- \frac{5}{\sqrt{378}} \vec{j}-\frac{8}{\sqrt{378}} \vec{k} \approx -0.87 \vec{i}-0.26 \vec{j}-0.41 \vec{k}\).
