Vektoriprojektio ja projektiovektori

Vektoriprojektio tai vektorin projektio on tärkeä käsite sellaisessa sovelluksissa, joissa etsitään lyhintä etäisyyttä suoralta johonkin pisteeseen. Vektoriprojektio laskemalla saadaan muodostettua projektiovektori. Se on olemassa aina kahden vektorin välillä: voidaan laskea vektorin \(\vec{a}\) projektio vektorille \(\vec{b}\) tai vektorin \(\vec{b}\) projektio vektorille \(\vec{a}\). Ensimmäistä tapausta merkitään \(\vec{a_b}\) ja jälkimmäistä \(\vec{b_a}\).

Seuraavan kuvan avulla voidaan esittää vektoriprojektiolle (tai projektiovektorille) määritelmä: Vektorin \(\vec{a}\) projektio vektorille \(\vec{b}\) eli \(\vec{a_b}\) on vektorin \(\vec{a}\) alkupisteestä alkava vektori, joka on

• yhdensuuntainen vektorin \(\vec{b}\) kanssa

• pituudeltaan sellainen, että piirtämällä kyseisen projektiovektorin kärjestä kohtisuora vektori \(\vec{a}_{\perp}\) päästään vektorin \(\vec{a}\) loppupisteeseen.

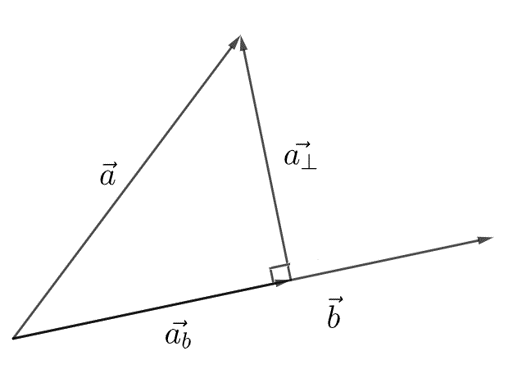
Edellisten ehtojen mukaisesti vektoriprojektioon tarvitaan vektori \(\vec{b}\), jota kerrotaan sopivalla kertoimella. Projektio lasketaankin kaavalla

\(\vec{a_b}=p\vec{b}\),

missä kerroin

\(p=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\) tai toisin ilmaistuna \(p=\frac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\)

on nimeltään skalaariprojektio. Skalaariprojektio on se luku, jolla vektori \(\vec{b}\) pitää kertoa, jotta sen kärjestä pääsee suorassa kulmassa vektorin \(\vec{a}\) kärkeen.

Skalaariprojektion laskukaavan perustelu

Vektoreista \(\vec{b}\) ja \(\vec{a_b}=p\vec{b}\) sekä vektoria \(p\vec{b}\) vastaan kohtisuorasta vektorista muodostuu suorakulmainen kulmio. Sovelletaan siihen suorakulmaisen kolmion trigonometriaa:

\(\text{cos}~\alpha = \frac{|p\vec{b}|}{|\vec{a}|}\)

Vektorin \(p\vec{b}\) pituus on \(|p\vec{b}|=p|\vec{b}\)|, joten

\(\text{cos}~\alpha = \frac{p|\vec{b}|}{|\vec{a}|}\),

josta voidaan ratkaista

\(p=\frac{|\vec{a}|}{|\vec{b}|}\text{cos}\alpha\).

Toisaalta pistetulon yhteydessä todettin, että \(\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|\text{cos}\alpha\), josta voidaan ratkaista

\(\text{cos}\alpha = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\)

Sijoitetaan tämä kaavaan \(p=\frac{|\vec{a}|}{|\vec{b}|}\text{cos}\alpha\):

\(p=\frac{|\vec{a}|}{|\vec{b}|}\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\)

Yhtälö sievenee muotoon

\(p=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|^2}\)

Lisäksi pistetulon määritelmän mukaisesti \(|\vec{b}|^2=\vec{b}\cdot \vec{b}\), joten \(p=\frac{\vec{a}\cdot\vec{b}}{\vec{b}\cdot\vec{b}}\).

Vektorin projektiota vastaan kohtisuora komponentti \(\vec{a_{\perp}}\) saadaan vähentämällä vektorista sen projektio, siis \(\vec{a_{\perp}}=\vec{a}-\vec{a_b}\). Tämän vektorin pituus on lyhin etäisyys vektorin \(\vec{a}\) kärjen ja vektorin \(\vec{b}\) määrittämän suoran välillä.

Esimerkki

a) Laske vektorin \(\vec{a}=4\vec{i}\) projektio vektorille \(\vec{b}=\vec{i}+\vec{j}\).

b) Laske vektoriprojektio \(\vec{a_b}\), kun \(\vec{a}=4\vec{i}-5\vec{j}\) ja \(\vec{b}=-6\vec{i}+2\vec{j}\).

Ratkaisu

a) \(\vec{a_b}=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|^2} \cdot \vec{b} = \frac{4\cdot 1 + 0\cdot 1}{1^2+1^2} \cdot (\vec{i}+\vec{j}) = \frac{4}{2} (\vec{i}+\vec{j})=2\vec{i}+2\vec{j}\)

b) \(\vec{a_b}= \frac{4\cdot (-6)+(-5)\cdot 2}{(-6)^2+2^2} \cdot (-6 \vec{i}+2\vec{j}) =\frac{-24-10}{40}\cdot (-6 \vec{i}+2\vec{j})\)

\(=-\frac{34}{40} \cdot (-6 \vec{i})-\frac{34}{40} \cdot 2 \vec{j}= \frac{204}{40} \vec{i}-\frac{68}{40} \vec{j} \approx 5.1 \vec{i}-1.7 \vec{j}\)

Esimerkki

Olkoot vektorit \(\vec{A}=8\vec{i}+6\vec{j}-\vec{k}\) ja \(\vec{B}=3\vec{i}-4\vec{j}+2\vec{k}\). Laske

a) vektorin \(\vec{A}\) projektio vektorille \(\vec{B}\).

b) vektorin \(\vec{A}\) vektoria \(\vec{B}\) vastaan kohtisuora komponentti.

Ratkaisu

a) \(\vec{A_B}=\frac{8\cdot 3+6 \cdot (-4)-1\cdot 2}{3^2+(-4)^2+2^2}\cdot (3\vec{i}-4\vec{j}+2\vec{k})\)

\(= \frac{24-24-2}{9+16+4} \cdot (3\vec{i}-4\vec{j}+2\vec{k})=-\frac{2}{29}\cdot(3\vec{i}-4\vec{j}+2\vec{k})\)

\(=-\frac{6}{29} \vec{i}+\frac{8}{29} \vec{j}-\frac{4}{29} \vec{k}\approx -0.207 \vec{i}+0.275\vec{j}-0.138\vec{k}\)

Tarkistus WolframAlphan komennolla: projection[{8,6,-1},{3,-4,2}]

b) \(\vec{A_{\perp}}=\vec{A}-\vec{A_B}=8\vec{i}+6\vec{j}-\vec{k}-(-0.207 \vec{i}+0.275 \vec{j}-0.138 \vec{k})\)

\(= (8+0.207) \vec{i}+(6-0.275) \vec{j}+(-1+0.138) \vec{k}=8.207 \vec{i} +5.725 \vec{j}-0.862 \vec{k}\)

Esimerkki

Jaa vektori \(\vec{a}\) kahteen komponenttiin, joista toinen on vektorin \(\vec{b}\) suuntainen ja toinen sitä vastaan kohtisuorassa, kun vektorit ovat seuraavat:

a) \(\vec{a}=1.5\vec{i}+0.5\vec{j}\) ja \(\vec{b}=2\vec{i}+2\vec{j}\),

b) \(\vec{a}=4\vec{i}+2\vec{j}\) ja \(\vec{b}=2\vec{i}+\vec{j}\).

Ratkaisu

a) \(\vec{a_b}=\frac{1.5\cdot 2+0.5 \cdot 2}{2^2+2^2} \cdot (2 \vec{i}+2 \vec{j})=\frac{4}{8}\cdot (2 \vec{i}+2\vec{j})=\vec{i}+\vec{j}\)

\(\vec{a_{\perp}}=\vec{a}-\vec{a_b}=1.5 \vec{i}+0.5\vec{j}-(\vec{i}+\vec{j})=1.5\vec{i}+0.5\vec{j}-\vec{i}-\vec{j}=0.5\vec{i}-0.5\vec{j}\)

b) \(\vec{a_b}=\frac{4\cdot 2+2\cdot 1}{2^2+1^2}\cdot (2\vec{i}+\vec{j})=\frac{10}{5} \cdot (2\vec{i}+\vec{j})=4\vec{i}+2\vec{j}\)

\(\vec{a_{\perp}}=\vec{a}-\vec{a_b}=4\vec{i}+2\vec{j}-(4\vec{i}+2\vec{j})=0\vec{i}+0\vec{j}\)

Miksi kohtisuoraa komponenttia ei ole olemassa? Huomataan, että vektori \(\vec{b}\) saadaan kertomalla vektori \(\vec{a}\) luvulla \(\frac{1}{2}\). Vektorit ovat siis samansuuntaisia.

Projektiovektorin sovellus

Projektiovektorin avulla voi selvittää lyhyimmän mahdollisen reitin jostakin pisteestä suoralle. Oletetaan, että suora kulkee kuvan mukaisesti pisteestä \(A=(a_x,a_y)\) pisteeseen \(B=(b_x,b_y)\), ja suoran lähistöllä on piste \(C=(c_x,c_y)\).

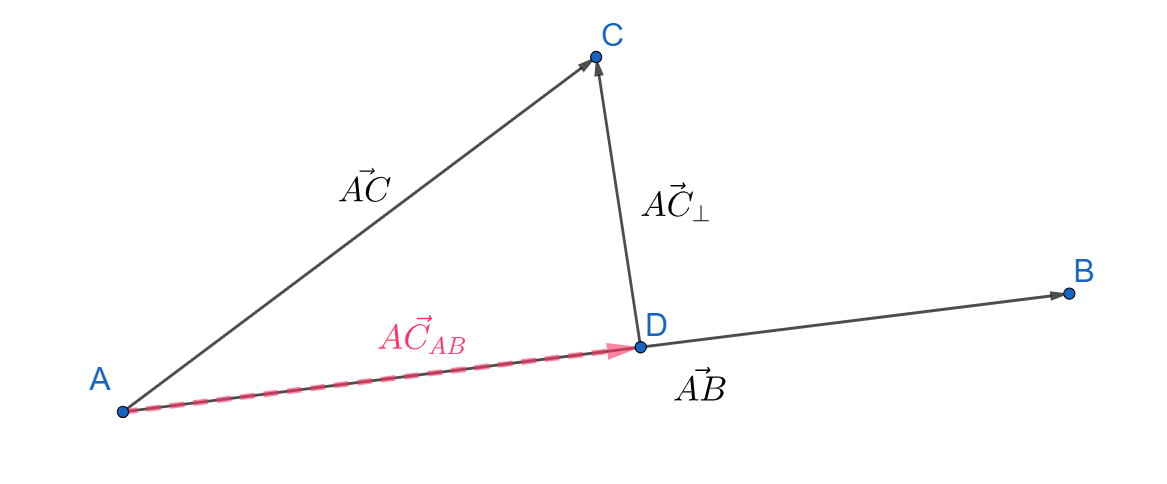
Muodostetaan seuraavat vektorit:

• suoraa kuvaa vektori \(\vec{AB} = (b_x-a_x) \vec{i} + (b_y-a_y) \vec{j}\)

• pisteiden \(A\) ja \(C\) välillä on vektori \(\vec{AC} = (c_x-a_x) \vec{i} + (c_y-a_y) \vec{j}\)

Lyhin etäisyys pisteestä \(C\) vektorille \(\vec{AB}\) on nyt \(\vec{AC_{\perp}}\). Se saadaan projektiovektorin avulla:

\(\vec{AC_{\perp}}=\vec{AC}-\vec{AC_{AB}}\).

Lopuksi voidaan selvittää, mihin suoran \(AB\) pisteeseen \(D\) pisteestä \(C\) on lyhin matka. Pisteen \(D\) paikkavektorin \(\vec{OD}\) saa lisäämällä pisteen \(A\) paikkavektoriin \(\vec{OA}\) projektiovektorin \(\vec{AC_{AB}}\):

\(\vec{OD}=\vec{OA}+\vec{AC_{AB}}\)

ja pisteen \(D\) koordinaatit saa suoraan paikkavektorista \(\vec{OD}\).

Tässä lasku on yksinkertaisuuden takia esitetty tason vektoreilla. Samat laskukaavat toimivat myös kolmessa ulottuvuudessa.

Esimerkki

Joki virtaa pisteestä \(A=(700,100)\) suoraan pisteeseen \(B=(1500,150)\). Joen vieressä pisteessä \(C=(1000,50)\) on talo, josta halutaan tehdä lyhin mahdollinen polku joen rantaan pisteeseen \(D\). Kuinka pitkä on kyseinen polku?

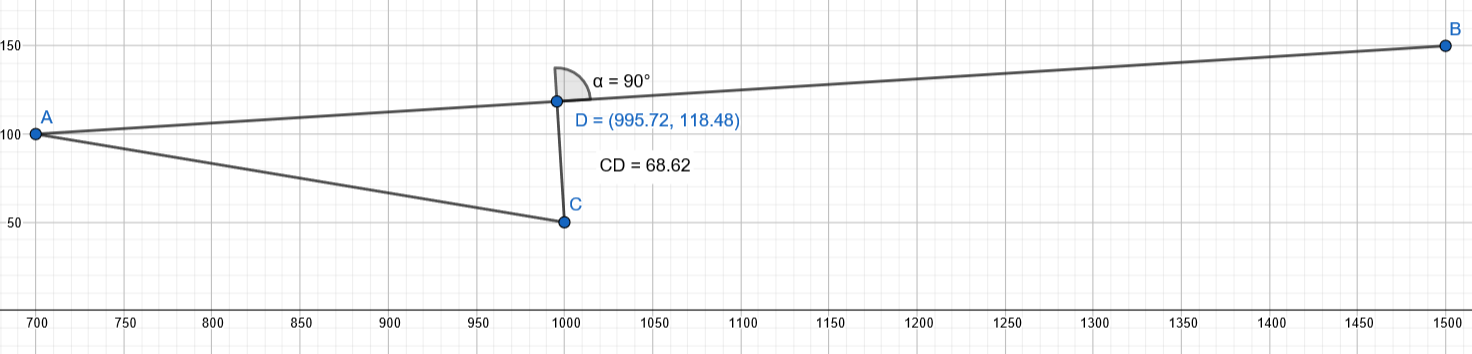
Ratkaisu

Muodostetaan aluksi pisteiden väliset vektorit:

Jokea kuvaava vektori on \(\vec{AB}=(1500-700)\vec{i}+(150-100)\vec{j} = 800 \vec{i} + 50\vec{j}\)

Joen alkupisteestä talolle vie vektori \(\vec{AC}=(1000-700)\vec{i}+(50-100)\vec{j} = 300\vec{i} – 50\vec{j}\)

Lyhimmän reitin löytämiseksi on laskettava vektorin \(\vec{AC}\) projektio vektorille \(\vec{AB}\), jonka jälkeen saadaan vektoria \(\vec{AB}\) vastaan kohtisuora vektori \(\vec{DC}\).

Skalaariprojektio on \(p=\frac{\vec{AC}\cdot \vec{AB}}{|\vec{AB}|^2} = \frac{800\cdot 300-50\cdot 50}{800^2+50^2} \approx 0.37\).

Projektiovektori on

\(\vec{AC_{AB}}=p\vec{AB}=0.37\cdot 800 \vec{i}+0.37\cdot 50\vec{j}=296 \vec{i}+18.5 \vec{j}\).

Polkua kuvaava vektori on

\(\vec{CD}=\vec{AC}-\vec{AC_{AB}}=(300-296) \vec{i}+(-50-18.5) \vec{j} = 4 \vec{i}-68.5 \vec{j}\).

Polun pituudeksi saadaan \(|\vec{CD}|=\sqrt{4^2+(-68.5)^2} \approx 68.6\).