Functions#
Note: this chapters is formed quickly from lecture notes. The figures are also missing.
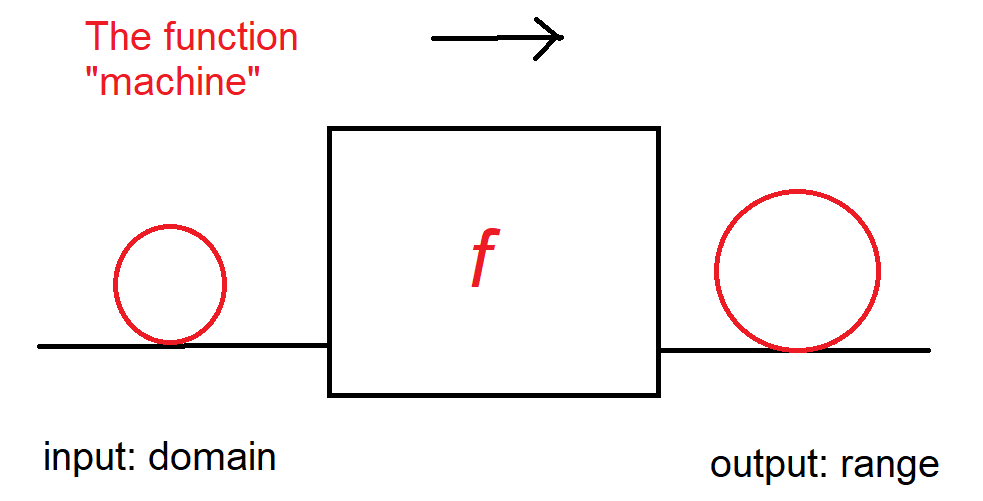
Fig. 10 The input to the factory is called the domain and the output is called the range.#
Linear functions#
Linear functions in the form of \(f(x)=ax+b\) are lines in (x,y)-plane, where \(a,b\in\mathbb{R}\), and the coefficient \(a\) is called the slope and the constant term \(b\) is the value of the intersection point with y-axis.
The slope, the coefficient in front of the variable \(x\), determines if our function is increasing or decreasing one, or horizontal (parallel with the x-axis).
if \(a > 0\), the function is increasing
if \(a < 0\), the function is decreasing
if \(a = 0\), the function is parallel with x-axis
For example a function \(f(x)=3x-1\) multiplies the variable \(x\) by three and subtracts one from the product.
Let’s consider another linear function of \(f(x)=-4x+10{,}\ x\in\mathbb{R}\)
The value of the function can be computed depending on the value of the variable \(x\).
\(f(0)=-4\cdot0+10=10\)
\(f(1)=-4\cdot1+10=6\)
\(f(2)=-4\cdot2+10=2\)
Judging from the value of the function, the function is a straight line and a decreasing one. This can be seen of course from the slope as well, which is negative.
Roots of a linear function#
The root is the intersection point with the x-axis. A linear function can have one, zero or infinite amount of roots.
If the domain of a linear function is not restricted and
\(a ≠ 0\), the there exists one and only root and the function looks like \(f(x)=ax+b\). If \(b = 0\), then the root is in the origin.
\(a = 0\) and \(b ≠ 0\), the there are no roots and the function looks like \(f(x)=b\).
\(a = 0\) and \(b = 0\), then there is infinite amount of roots and the function looks like \(f(x)=0\).
How to find the root?
The root represents the coordinate point, where \(f(x)=0\), which is the same as the intersection point with x-axis. In other words, our goal is to find out the value for variable \(x\), when the function has a value of zero.
Write down the equation and solve it. \(\begin{align}f(x)&=0 \\ -4x+10&=0 \\ -4x&=-10\ \parallel:(-4) \\ x&=\frac{5}{2} \end{align}\)
The root of the function \(f(x)=-4x+10{,}\ x\in\mathbb{R} \) is \(x=\frac{5}{2}\).
Inequality of a linear function#
For a linear functio \(f(x)=-4x+10{,}\ x\in\mathbb{R}\), inequality means that we look for a domain that satisfies the inequality.
For example \(f(x)\gt 0\), when \(x\lt \frac{5}{2}\), since the slope < 0.
\(\begin{align}f(x)\gt& 0 \\ -4x+10\gt& 0 \\ -4x\gt& -10\ \parallel: (-4) \\ x\lt& \frac{5}{2} \end{align}\)
Another example: \(f(x)=5x+2\)
\(\begin{align}f\left(x\right)\le& 5 \\ 5x+2\le& 5 \\ 5x\le& 3\ \parallel:5 \\ x\le& \frac{3}{5} \end{align}\)
Restricted domain#
Example
\(\begin{align}f(x)=&2x-2{,}\ x\ge4 \\ f(x)\gt& 0 \\ 2x-2\gt& 0 \\ 2x\gt& 2\ \parallel:2 \\ x\gt& 1 \end{align}\)
So \(f(x)>0\) when \(x\gt 1\), but the correct answer is \(x\ge4\), since the domain is \(x\ge4\).
